![]() Espacios. Vol. 36 (Nº 14) Año 2015. Pág. E-1
Espacios. Vol. 36 (Nº 14) Año 2015. Pág. E-1
Nuevas experiencias e innovaciones en la enseñanza de leyes de conservación y simetrías en asignaturas de física para cursos de ingeniería
Experiences and innovations on teaching conservation laws and symmetries to enginnering courses
Nestor Cortez SAAVEDRA-FILHO 1; Arandi Ginane BEZERRA-JR 2; Gustavo A. GIMENÉZ-LUGO 3
Recibido: 01/04/2015 • Aprobado: 23/05/2015
Contenido
RESUMO: La enseñanza de Mecánica es comúnmente presentada bajo la forma de contenidos aislados, con una sucesión de conceptos que dan a entender que la teoría ya apareció "lista". Con frecuencia existen rupturas en el desarrollo de los contenidos, cuando algunas Leyes de Conservación aparecen sin motivos muy claros. Este trabajo tiene por objetivo exponer algunas experiencias e innovaciones en la enseñanza distas Leyes, a través del paralelo con las simetrías asociadas. Tal práctica ha sido utilizada en las asignaturas de Mecánica para los cursos de Ingeniería de la Universidad Tecnológica Federal de Paraná donde pudimos notar un aumento tanto en el interés de los alumnos cuanto en la profundidad de las discusiones en sala de clase. |
ABSTRACT: In this paper we discuss some experiences and innovations about how to teach conservations laws such as energy and momentum at Classical Mechanics classes for engineering students. Instead of a traditional and amusing way, this work shows a ludic and interdisciplinary one, in order to show to the students that symmetries and conservation laws are related and, furthermore, symmetries are not an application to reduce algebraic calculations, but a fundamental brick on Mechanics theory. |
1. Introducción
La enseñanza de Mecánica en el Brasil continua siendo muy tradicional, pese a algunas tentativas como el GREF (Grupo de Reestructuración de la Enseñanza de Física, 1990). Bajo esa perspectiva la secuencia de contenidos siempre comienza con cinemática, pasando después para dinámica, enunciando primero las Leyes de Newton de manera más restricta, haciendo referencia a la aceleración en lugar de la cantidad de movimiento, siendo esta una tentativa de hacer de la aceleración una especie de "eslabón perdido" entre la cinemática y la dinámica. Al terminar el estudio de la Leyes de Newton, el alumno tiene la percepción de que ellas representan la plenitud en Mecánica: tal vez los libros sobre esta asignatura deberían terminar allí, dada la manera en que el concepto de energía aparece justo enseguida, casi como si fuera una mera extensión del concepto de trabajo realizado por una fuerza. Se pierde allí una excelente oportunidad de hacer con que los estudiantes perciban la necesidad y la existencia de una formulación más amplia de la Mecánica Clásica, siéndoles negado el concepto de que algunas magnitudes físicas de un sistema permanecen, en su totalidad, conservadas (constantes) y que la manera en que tal magnitud se distribuye en un sistema de modos diferentes puede determinar su evolución.
La enseñanza de la percepción de simetrías en Física también es negligenciada. Con frecuencia las simetrías son citadas apenas cuando pueden auxiliar en cálculos matemáticos, como en la simplificación de una integral o en alguna relación trigonométrica. Esto lleva al estudiante a pensar en las simetrías apenas como un artificio matemático "facilitador de cálculos". Entretanto, el estudio de las propiedades de simetría de un sistema puede brindar informaciones valiosas sobre el mismo, como por ejemplo la forma de las soluciones de las ecuaciones de movimiento o las reducciones de grados de libertad. En otras palabras, las propiedades físicas de simetría son las que determinan las eventuales simplificaciones matemáticas, pues ellas, por sí mismas, carecen de sentido físico.
2. Propuesta de trabajo
La primera etapa de la aplicación de esta propuesta fue la identificación de los subsunsores de que dispondrían los estudiantes para asimilar el tema de simetrías y conservaciones. De tal modo, por medio de discusiones en sala de clase, casi siempre eran citadas estructuras como esferas y espejos (simetrías), así como energía (conservación). En el último caso, la conservación de la energía mecánica parece ser un tema bien establecido entre estos estudiantes (tercer año de Ingenierías) dado que es un tema abordado en Física con ellos desde la Enseñanza Secundaria. En este punto la tentativa fue causar impacto exponiendo la noción de que ni la simetría de la imagen ofrecida por un espejo plano es perfecta, así como también explorando el aspecto lúdico de mostrar una simetría "escondida" en una obra de arte bien conocida. De tal manera se intentó posicionar en discusiones prácticas la idea de que la simetría no es algo metafísico y sí un concepto palpable al cual se puede dar un uso práctico, colocándose por ejemplo que varias de las aplicaciones de los objetos esféricos en lo cotidiano provienen de sus propiedades de simetría. En este momento las propiedades de simetría fueron abordadas desde un punto de vista más sensorial (ver, sentir). En la tentativa de promover la asimilación, los desarrollos matemáticos del tema eran siempre acompañados de experimentos previamente montados en los laboratorios de Física. La cuestión central era siempre la misma: acabamos de ver una relación entre simetría y conservación de alguna magnitud física (energía mecánica, cantidad de movimiento), entonces, ¿cómo se puede elaborar un experimento para mostrar la relación entre ellas ? En este punto el riel de aire, presente en gran parte de los laboratorios de enseñanza de física de las instituciones de enseñanza superior, fue bastante útil para que los propios estudiantes propusieran los experimentos para mostrar que:
1) Una simetría espacial (trayectoria recta e horizontal en el riel de aire) hacia que el carrito deslizando mantuviera su cantidad de movimiento constante. Una asimetría (curva, plano inclinado) alteraba el valor de la cantidad de movimiento, alejándola de su conservación.
2) Una simetría temporal (desplazamientos iguales en intervalos de tiempo iguales) mantenía la velocidad y por lo tanto la energía cinética constante.
3) En el caso de la rotación, el profesor tuvo que intervenir más, debido al sutil carácter vectorial de este tipo de movimiento. Al fin, la conservación del momento angular fue propuesta y demostrada en el experimento de un estudiante sentado en una silla giratoria aferrando una rueda de bicicleta en el plano horizontal. Al ser invertido el plano de rotación de la rueda la silla comenzaba a girar en sentido contrario. A partir de estas discusiones matemáticas y sus consecuentes demostraciones prácticas fue más fácil elevar el grado de asimilación de este concepto por los estudiantes. Finalmente fueron propuestos algunos ejercicios teóricos que incluían deducciones y cálculos para verificar si hubo (como puede ser observado en estos ejercicios y sus discusiones) un aumento real el el aprendizaje de los estudiantes.
Pasemos ahora a la demostración de algunos pasos de la discusión en sala de clase y laboratorios. El lector debe efectuar la asociación entre aquello que está siendo expuesto y a dónde los profesores pretendían llegar en cada discusión.
¿Qué son simetrías?
La simetría puede ser definida de dos maneras distinta. Una tiene relación con un concepto estético, da la idea de proporcionalidad. Otra manera tiene que ver con la existencia de un patrón que puede ser demostrado formalmente para un determinado sistema bajo estudio. Es a este último caso que nos referimos cuando hablamos de simetrías en Física. El caso de observación más simple de simetría tal vez sea el de una esfera, donde aparece simetría de rotación, por ejemplo, para cualquier eje que sea diametral a la esfera. Con frecuencia pensamos en imágenes reflejadas por un espejo plano como un caso perfecto de simetría. Empero, la simetría aquí no es perfecta: como las imágenes son enantiomorfas hay una inversión derecha-izquierda en las imágenes reflejadas (Figura 1).

Figura 1: La imagen enantiomorfa generada por un espejo plano.
Otros casos de simetrías son más sutiles: en el cuadro "La Gioconda" (Mona Lisa), de Leonardo da Vinci, ¿Usted conseguiría identificar alguna simetría? ¡Aparentemente no! Pero aquí Da Vinci utilizó un "truco" frecuente en sus obras y en la de otros renacentistas: hay un punto de simetría escondido en la pintura. Al observar con cuidado el ojo izquierdo de la Mona Lisa, ¡el mismo está exactamente sobre la recta vertical que divide la pintura en su mitad! (Figura 2)

Figura 2: "La Gioconda" de Leonardo da Vinci.
A pesar de no ser este un artículo sobre Arte Renacentista, queda la lección: a veces algunas simetrías no son fácilmente observadas a primera vista, lo cual no significa que el sistema en cuestión no la posea y por tanto sea de solución más difícil. Es habitual que podamos desvelar alguna propiedad de simetría de un sistema observándolo de manera diferente, como por ejemplo a través de un cambio de variables o sistema de coordenadas, ya que las leyes de Física son invariantes para tales transformaciones, de acuerdo a uno de los postulados de la Relatividad Restricta.
Simetrías en Física
Más allá de lo que será discutido formalmente en este artículo, el concepto de simetría ha inspirado diversos trabajos en Física (FEYNMANN, 1967). A veces, el físico no tiene un punto de partida "formal" para un postulado, pero, por intuición, generalmente asociada a alguna simetría observable, se ha llegado a resultados notables en la Historia de la Física.
Un caso interesante fue cuando el físico ruso Dmitri Mendeleiev, observando propiedades periódicas (por lo tanto, con una simetría embutida), llegó a la formulación de la Tabla Periódica de los Elementos, prácticamente en la forma como la conocemos hoy en día. Con la aparición de la Mecánica Cuántica, tales propiedades periódicas y simétricas de los elementos fueron aclaradas, lo que sirvió para enaltecer aún más el mérito de la intuición de Mendeleiev.
Otro caso se dio en la evolución del Electromagnetismo. La búsqueda por la unificación entre los fenómenos eléctricos y magnéticos sufrió un gran impulso con el descubrimiento proporcionado por el experimento de Hans Christian Oersted, que probó que el efecto de una corriente eléctrica podría influenciar la orientación de una brújula, un efecto de carácter magnético. A partir de allí hubo una corrida buscando una explicación formal sobre la simetría de eses fenómenos. Aquí, con argumentos iniciales basados en simetría, James Clerk Maxwell relacionó la Ley de Faraday con la Ley de Ampère, vistas en las Ecuaciones (1) y (2), respectivamente:


La Ecuación (1) establece que una variación en el campo magnético genera un campo eléctrico rotacional (por lo tanto, de líneas de campo cerradas) alrededor de las líneas del campo magnético. Una representación diste facto puede ser vista en la Figura 3:
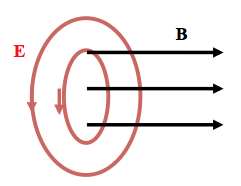
Figura 3: Ley de Faraday.
Ya la Ecuación (2) establece que un campo magnético también rotacional (aquí las líneas de campo siempre son cerradas, debido a la inexistencia de monopolos magnéticos) apenas es generado alrededor de una corriente eléctrica, J es la densidad de corriente. Bien, Maxwell se cuestionó sobre si no habría un caso de campo eléctrico variable que generase un campo magnético, o sea, esto sería el caso de "viceversa" entre las leyes de Faraday y Ampère. Maxwell realizó entonces el experimento con un campo eléctrico variable, obtenido durante el proceso de carga (o descarga) de un condensador. De hecho, utilizando argumentos de simetría y de continuidad del campo magnético, Maxwell encontró el término de campo eléctrico variable para completar la Ley de Ampère, llamándola de "corriente de desplazamiento" (Figura 4).
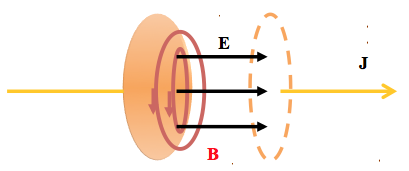
Figura 4: La "corriente de desplazamiento" de Maxwell en un condensador siendo cargado.
Así, la Ley de Ampère completa puede ser escrita como en la Ecuación (3):

Con esto tenemos un ejemplo más donde la intuición física, basada en argumentos de simetría, tuvo una contribución decisiva en la formulación de las leyes fundamentales de Física.
Leyes de Conservación y sus relaciones con propiedades de simetría
Este artigo supone que los estudiantes ya han tenido contacto con las tres principales leyes de conservación en Mecánica Clásica, siendo ellas (NUSSENSZVEIG, 1981):
Conservación del Momento Lineal: en ausencia de fuerza resultante externa, el momento lineal total de un sistema permanece constante.

Donde P = mv representa la cantidad de movimiento total del sistema. Si el lado izquierdo de la Ecuación (4) es nulo, resulta que P es una constante de movimiento.
Conservación del Momento Angular: en ausencia de torque resultante externo, el momento angular total de un sistema permanece constante.

Donde L = r x P representa el momento angular total del sistema. Nuevamente, si el lado izquierdo de la Ecuación (5) es nulo, L también es una constante de movimiento.
Conservación de la Energía Mecánica: en ausencia de fuerzas disipadoras, la energía mecánica de un sistema es conservada. Con relación a esta última ley de conservación, existen algunas consecuencias fundamentales que vamos a detallar, pues su extrapolación será importante para aquello que queremos discutir en este artículo. Más allá de ello, la influencia de la Conservación de Energía puede ser extrapolada para otros tipos de sistemas, como en Mecánica de los Fluidos (ecuación de Bernoulli), Termodinámica (1ª Ley) y Electricidad (Ley de las Mallas en circuitos eléctricos) (FEYNMANN, 1963). La generalización de tal ley de conservación es realizada en (NUSSENSZVEIG, 1981), lo que lleva directamente a:

Donde U es la energía del sistema, F es una de las fuerza aplicadas al sistema, Δr es el desplazamiento del punto de aplicación de cada fuerza.
Ahora estamos aptos a discutir la relación íntima entre las Leyes de Conservación y simetrías, aplicando propiedades de simetría en la Ecuación (6). Decimos que un sistema tiene una propiedad de simetría cuando no es alterado al efectuar sobre el una operación correspondiente a esta simetría. Pasemos, por lo tanto, a la discusión sobre las simetrías.
Uniformidad Temporal y Conservación de la Energía
Si las fuerzas externas que actúan sobre un sistema no dependen del tiempo (uniformidad temporal), resulta que la tasa de variación de la energía con el tiempo es nula, llevando la Ecuación (6) a presentarse como:

El último término de la Ecuación (7) es la potencia, que es la tasa de variación temporal con que un trabajo es realizado. Según el teorema del trabajo y energía cinética (K), resulta que el trabajo de la fuerza resultante es igual a la variación de energía cinética. De este modo podemos reescribir la Ecuación (7) como:

Pues bien, como la energía mecánica E = K + U, tenemos finalmente que:

Que es la conocida Ley de la Conservación de la Energía Mecánica. De esta manera, una simetría temporal implica en la Conservación de la Energía Mecánica de este sistema.
Homogeneidad Espacial y Conservación del Momento Lineal
Ahora vamos a estudiar simetrías con relación a traslaciones en el espacio homogéneo. Desplazando un sistema completo por un desplazamiento ∆R tenemos que la Ecuación (6) se torna:

Donde suponemos aquí que el potencial depende explícitamente del tempo, recayendo en el caso anterior. De hecho, para que la expresión anterior sea nula, solo hay una posibilidad, pues el desplazamiento ∆R obviamente no es nulo, luego, la sumatoria de las fuerza deberá ser nula de modo a tornar válida la Ecuación (10). Pero, de acuerdo con la segunda Ley de Newton,

Donde la sumatoria de las fuerzas indica la suma sobre todas las fuerzas externas sobre el sistema y P es el momento lineal del sistema como un todo. Como la expresión dada es nula, de acuerdo con (11), tenemos entonces que P = constante, luego el momento lineal de un sistema es conservado cuando sufre una traslación espacial (el espacio es homogéneo).
Isotropía Espacial y Conservación del Momento Angular
Para que hallemos la última ley de conservación, que respecta al momento angular, debemos recordar la representación vectorial de las magnitudes angulares asociadas al movimiento de rotación. Un desplazamiento angular ∆θ corresponde a un desplazamiento lineal ∆r, cuya relación es dr = dθ x r. La justificación para esta relación puede ser vista en la Figura 5.
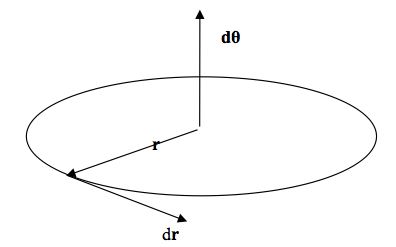
Figura 5: Relación entre las magnitudes vectoriales de rotación.
Así, la Ecuación (6) queda escrita como:

Utilizando la propriedad que envuelve productos escalares y vectoriales, nada más recordando:

La Ecuación (12) se vuelve:
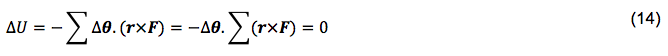
De hecho, obviamente ∆θ no es nulo, entonces nos sobra que:

Pero esta última expresión es exactamente el torque externo resultante, actuando sobre el sistema. De este modo tenemos que la Ecuación (16), en conjunción con la segunda Ley de Newton para la rotación, implica en:

Donde L es el momento angular total del sistema, es una constante del movimiento. Así, una isotropía espacial (rotación), implica en la conservación del momento angular de un sistema.
Todas las discusiones anteriores pueden ser resumidas en un teorema enunciado por la matemática Emmy Noether en 1915 (GOLDSTEIN, 1980):
A cada ley de conservación corresponde una simetría y viceversa.
Citamos la fecha del teorema para que los estudiantes no piensen que estamos apenas discutiendo una forma de Física que fue elaborada hace mucho tiempo. En la siguiente sección, vamos a fijar la mirada más allá. Realmente, veremos que las consecuencias del Teorema de Noether no solo son aplicables a la Física Clásica. Un resumen de las discusiones desarrolladas hasta aquí puede ser visto en la Tabla 1:
Tabla 1: Leyes de Conservación y propiedades de simetría para un sistema aislado
Condición |
Consecuencia |
Simetría |
El potencial no depende del tiempo |
Energía Mecánica es conservada |
Temporalmente |
La resultante de las fuerzas externas es nula |
Momento Lineal es conservado |
Traslacionalmente, espacio homogéneo
|
La resultante de los torques externos es nula |
Momento Angular es conservado
|
Rotacionalmente, espacio isotrópico
|
Variables canónicamente conjugadas
Existe una formulación más avanzada para la Mecánica Clásica en relación a aquella que discutimos en este trabajo. Ella es la formulación hamiltoniana, que trabaja con una función, el hamiltoniano, que describe el comportamiento de la energía en la evolución de un sistema físico. Las Leyes de Simetría reciben un formalismo más profundo en esta formulación, donde existe el concepto de magnitudes canónicamente conjugadas. Esto puede ser transpuesto para la Mecánica Cuántica, donde las magnitudes observables son encaradas como operadores. Aquí, apenas citaremos los operadores para energía y momento lineal (CARUSO e OGURI, 2006):


Donde h es la constante de Planck. Como puede notarse, el operador energía envuelve una operación con relación al tiempo y el operador momento lineal hace lo mismo en relación a x. Entonces, en el formalismo hamiltoniano llevado a la Mecánica Cuántica, las magnitudes canónicamente conjugadas son aquellas relacionadas a través de una ley de conservación y su respectiva simetría. Y aún más allá: en Mecánica Cuántica es dicho que tales magnitudes no pueden ser observadas simultáneamente, lo que resulta en el famoso Principio de la Incertidumbre, enunciado por Werner Heisenberg en 1927. El Principio de la Incertidumbre establece que: 
Así, no solo las variables canónicamente conjugadas forman operadores cuánticos o están conectadas por simetrías y conservaciones, sino que está en la propia estructura de la naturaleza la incapacidad de obtener observaciones de estos pares de magnitudes con total precisión simultáneamente!
3. Conclusión
La propuesta de este artículo fue presentar las leyes de conservación y sus relaciones con propiedades de simetrías del espacio, con la intención de aumentar la visión global del alumno sobre el asunto. Inicialmente, la definición de simetría es presentada de forma lúdica, con alusión a objetos y obras ya conocidas por los estudiantes, como es el caso de la corriente de desplazamiento de Maxwell. Esto coloca las propriedades de simetría como algo que ya fue utilizado por los estudiantes con suceso, lo que les permite hacer relaciones transversales entre los contenidos ya estudiados, como es el caso aquí entre Electromagnetismo y Mecánica Clásica, más allá de relacionarlos con tópicos de Física Moderna, algo que siempre motiva e despierta el interés de los estudiantes. |Esto crea una contextualización que sirve para despertar el interés de los mismos, que pasan a ver los términos "conservación" y "simetría" no como algo complejo y fuera de su comprensión, sino todo lo contrario, como algo que puede ser visto cotidianamente en sus realidades. Los resultados de esta aplicación han encontrado gran receptividad de parte de los estudiantes, lo que ha motivado bellas discusiones y cuestionamientos de parte de los mismos en sala de clase. Esto ha transformado un tópico de la asignatura constantemente tratado como siendo poco motivador para ellos, en una gran oportunidad de enriquecer el proceso de enseñanza-aprendizaje.
Referencias
CARUSO, F. OGURI, V. Física Moderna. Campus Editorial. Rio de Janeiro, Brasil (2006).
FEYNMAN, R.; LEIGHTON, R.; SANDS, M. The Feynman Lectures on Physics, vol 1. Addison-Wesley, Reading, EE.UU (1963).
FEYNMAN, R, The Character of Physical Law. MIT Press, Boston, EE.UU (1967).
GOLDSTEIN, H. Classical Mechanics, 2ª edición. Addison-Wesley, Reading, EE.UU (1980).
GREF. Física 1 – Mecânica. Editora da Universidade de São Paulo, São Paulo, Brasil (1990).
NUSSENZVEIG, H. M. Curso de Física Básica, vol. 1: Mecânica. Edgard Blücher, São Paulo, Brasil (1981).
1. Universidade Tecnológica Federal de Paraná, Departamento Académico de Física. Curitiba – Paraná, Brasil. Email: nestorsf@utfpr.edu.br
2.
Universidade Tecnológica Federal de Paraná, Departamento Académico de Física. Curitiba – Paraná, Brasil. Email: arandi@utfpr.edu.br
3. Universidade Tecnológica Federal de Paraná, Departamento Académico de Física. Curitiba – Paraná, Brasil. Email: gustavo@dainf.ct.utfpr.edu.br