

Vol. 38 (Nº 31) Año 2017. Pág. 4
Gabriel Alberto AGUDELO Torres 1; Luis Ceferino FRANCO Arbeláez 2; Luis Eduardo FRANCO Ceballos 3; Nora GAVIRA Durón 4
Recibido: 17/01/2017 • Aprobado: 12/02/2017
RESUMEN: En este artículo se presenta un modelo para estimar las implicaciones económicas que tendría la salida del Reino Unido de la Unión Europea. Aplicando procesos de Itô económicamente ponderados combinados se modela la dinámica estocástica del precio del dólar estadounidense sujeto a las diferentes fuerzas que afectan su precio relativo con otras monedas en diferentes mercados regionales. Los países que se utilizan como muestra para modelar el precio relativo del dólar con respecto de monedas locales son: Australia, Canadá, República Checa, Dinamarca, China (Hong Kong), Japón, México, Noruega, Polonia, Rusia, Singapur, Sudáfrica, Suecia, Suiza, Turquía, Reino Unido y pertenecientes a la Zona Euro. Para el cálculo de la matriz de ponderaciones se utiliza la distancia económica (no geográfica) entre las regiones, y como indicador de la relación entre cada pareja de regiones se considera el flujo comercial entre ellas. Se concluye que ante una disminución del 20% en el flujo comercial entre el Reino Unido y la Zona Euro y un aumento del 15% entre el primero y sus socios más cercanos, Noruega y Suiza, contrario a lo esperado, el precio del euro y de la libra esterlina no sufrirían gran variación (entre 2% y 3% en un periodo de cuatro años). |
ABSTRACT: In this article a model is presented in order to estimate the economic repercussions of an exit of the United Kingdom from the European Union. Through the application of Itô's economically weighted processes combined, the stochastic dynamic of the price of the American dollar is modeled, subject to the different forces that affect its price, in comparison to other currencies in different regional markets. The countries used as samples to model the relative price of the dollar in comparison to local currencies are: Australia, Canada, Czech Republic, Denmark, China (Hong Kong), Japan, Mexico, Norway, Poland, Russia, Singapore, South Africa, Sweden, Switzerland, Turkey, the United Kingdom and those belonging to the Eurozone. For the calculation of the weighted matrix, the economic distance (not geographic) among the regions is used, and as an indicator of the relation between each pair of regions, the trade flow between them is considered. It is concluded that in case of a 20% decrease in the flow of trade between the United Kingdom and the Eurozone and a 15% increase between the former and its closest partners, Norway and Switzerland, contrary to expectations, the price of the euro and the British Pound would not suffer great variation (between 2% and 3% in a four year period.) |
En 1957 la República Federal de Alemania, Bélgica, Francia, Italia, Luxemburgo y los Países Bajos forman la Comunidad Económica Europea (CEE). El 1 de enero de 1973 se anexa el Reino Unido, junto con Dinamarca e Irlanda (EUR-Lex, 2016). En la década de los 80 del siglo pasado se fueron integrando más países, hasta que en 1992 se promulgó del Tratado de la Unión Europea. Este tratado marcaba la pauta para la creación de una moneda única (Euro) e indicaba las condiciones para que los países miembros pudieran adoptarla (EUR-Lex, 2016). El 1 de enero de 1999, el euro fue adoptado como la moneda de 11 de los 13 países miembros de la Unión; el 1 de enero de 2002 los billetes y monedas de 13 de los 15 países que formaban la Unión Europea fueron reemplazados por Euros (Banco Central Europeo, 2016), mientras que Dinamarca y el Reino Unido optaron por la cláusula de “exclusión voluntaria” contemplada en el Tratado (UE, 2010) y decidieron continuar con su moneda local. A partir del 1 de julio de 2013, la Unión Europea está formadas por 28 países.
El término Brexit se genera de la abreviatura de Britain (Gran Bretaña) y exit (salida), significa la salida del Reino Unido de la Unión Europea (UE), y fue adoptado de la iniciativa de la posible salida de Grecia de la UE en 2012 (Grexit). Desde que David Cameron (primer ministro Inglés hasta junio de 2016), prometió en su campaña política de 2013, la realización de un referéndum para que la población decidiera si permanecían o salían de la UE (Brexit), diversas investigaciones indican que la salida tendría repercusiones importantes para el Reino Unido y el resto del mundo, y afirman que durante décadas el nivel económico del Reino Unido se verá afectado debido a que la Unión Europea es su mayor socio comercial y su salida de la UE bajará el comercio, así como la inversión extranjera directa (IED), y se presentará una caída en la inmigración; y esto puede conducir a niveles de vida más bajos para los nacidos en el Reino Unido, ya que los inmigrantes ayudan a reducir el déficit. (Breinlich, y otros, 2016).
De ser materializado el Brexit traería como consecuencia un gran impacto en términos de pérdida del bienestar de los Británicos y en la caída de la inversión extranjera directa (Boulanger & Philippidis, 2015), (Weiler, 2015); según Barrett, Bergin, FitzGerald, Lambert, McCoy, Morgenroth y Studnicka (2015) la salida de Reino Unido de la UE afectará negativamente la economía de Irlanda, ya que es su principal socio comercial. Möller & Oliver (2014) analizan las posibles consecuencias del Brexit para los países miembros de la UE, de forma individual, Europa en general y otros países, como Estados Unidos y Japón. En general todos los países de la UE perderían ingresos importantes después del Brexit y además se impactarían los mercados financieros de todo el mundo.
Sin embargo, el 23 de junio de 2016 se llevó acabo dicho referéndum y los resultados arrojaron que se llevaría a cabo el Brexit, con base en el Artículo 50 de la Versión Consolidada del Tratado de la Unión Europea, el cual indica que: “1. Todo Estado miembro podrá decidir, de conformidad con sus normas constitucionales, retirarse de la Unión” (DOUE, 2012). Posterior a su aprobación, David Cameron, anunció su renuncia, lo que resulta un duro golpe para las 28 naciones que forman la UE y generó incertidumbre sobre el comercio y la inversión entre los países miembros, y conmocionó a los mercados financieros; varios diarios internacionales sugieren que Londres dejará de ser la capital europea del dinero y grandes capitales emigrarán a ciudades como New York, Frankfurt o París, donde inversiones inmobiliarias (Lash, 2016) y de seguros encontrarán nuevos mercados (Howell, 2016); prueba de ello son las noticias del 6 de septiembre de 2016 sobre la caída del sector inmobiliario en Londres a partir de la consulta Brexit (Wallace, 2016). El 13 de julio de 2016 la ministra Theresa May, asumió el cargo de primera ministra del Reino Unido, con la promesa de dirigir las negociaciones para la salida del Reino Unido de la UE.
Por otra parte, diversas investigaciones dedicadas a estudiar la dinámica estocástica de precios de activos financieros en una región o mercado en particular, suponen que dichos precios se comportan de acuerdo con un proceso de Itô. Los trabajos seminales de este enfoque son, por supuesto, Black y Scholes (1973), Merton (1973), Vasicek (1977), y Cox Ingersoll y Ross (1985a) y (1985b). Otros trabajos que generalizan los procesos de Itô se encuentran en Grinols y Turnovsky (1993), Schmedders (1998) y Venegas (2001), (2006a) y (2006b), entre otros.
Al considerar un activo que se negocia en ![]() regiones diferentes y que en cada región está sujeto a diferentes fuerzas que afectan su precio, su modelación también debería tomar en cuenta que los diferentes mercados regionales podrían estar o no interrelacionados. Incorporar estos aspectos en la modelación del precio del activo financiero no sólo indica una sofisticación teórica, sino también representa un aspecto relevante que agrega mayor realismo al modelado y permite la simulación de su dinámica ante cambios en la forma en que se relacionan las regiones.
regiones diferentes y que en cada región está sujeto a diferentes fuerzas que afectan su precio, su modelación también debería tomar en cuenta que los diferentes mercados regionales podrían estar o no interrelacionados. Incorporar estos aspectos en la modelación del precio del activo financiero no sólo indica una sofisticación teórica, sino también representa un aspecto relevante que agrega mayor realismo al modelado y permite la simulación de su dinámica ante cambios en la forma en que se relacionan las regiones.
Por otro lado, la estadística espacial permite analizar los efectos regionales en la modelación de las variables; véanse, al respecto, Morán (1948), Geary (1954), Paelinck y Klaasen (1979). En ese sentido la econometría espacial se puede considerar como un complemento natural de la modelación estocástica del activo financiero con el fin de incorporar en su dinámica el hecho que pueda ser negociado en distintos mercados, y que ellos puedan estar interrelacionados o no.
En la modelación de activos financieros y su efecto espacial en las regiones vecinas se puede considerar el estudio de Ali y Kestens (2006) que analiza la relación y el contagio entre crisis cambiarias y sus determinantes, utilizando regresiones geográficamente ponderadas (GWR por sus siglas en inglés). Además, Ali y Lebreton (2013) estudian la difusión espacial de los ataques especulativos durante la caída del sistema de Bretton Woods. Sin embargo, estos autores no incluyen procesos de Itô en la modelación del precio del activo financiero. En este artículo se presenta un proceso estocástico de Itô para modelar el precio de un activo financiero que es negociado en diferentes mercados con potenciales correlaciones económicas, incorporadas en el modelo mediante técnicas de econometría espacial. Para ello se considera un activo financiero negociado en diversos mercados regionales y cuyos precios se suponen influenciados por condiciones internas de cada región, pero también por condiciones externas de las demás regiones. Es así como el precio del activo, además de estar afectado por la oferta y la demanda internas, estará influenciado por las condiciones de mercado en las regiones cercanas en términos económicos.
En este artículo el activo en cuestión es una divisa, el dólar estadounidense, y su precio relativo se modelará con respecto de la moneda de cada uno de los siguientes países: Australia, Canadá, República Checa, Dinamarca, China (Hong Kong), Japón, México, Noruega, Polonia, Rusia, Singapur, Sudáfrica, Suecia, Suiza, Turquía, Reino Unido y los países correspondientes a la Zona Euro tenidos en cuenta como un único país. Para modelar el precio de dólar estadounidense, sujeto a las diferentes fuerzas que afectan su precio relativo con otras monedas en diferentes mercados regionales que están interrelacionados, se utilizan los procesos de Itô económicamente ponderados combinados con la econometría espacial. Para el cálculo de la matriz de ponderaciones se emplea la distancia euclidiana entre las regiones analizadas, y como indicador de la relación entre cada pareja de regiones se utiliza la balanza comercial entre ellas (flujo comercial) medidas en miles de dólares; siendo el flujo comercial la variable que define la posición relativa de cada región.
Este artículo está organizado de la siguiente manera: en la Sección 2 se presenta la metodología, en la cual se desarrolla el modelo, se realiza la estimación de los parámetros y el cálculo de las ponderaciones económicas; luego, en la Sección 3, se considera el precio del dólar estadounidense con respecto de la moneda local de 17 regiones y se desarrolla una simulación de los efectos que un nuevo orden comercial produciría entre los países analizados; por último, en la Sección 4 se presentan algunas conclusiones.
A continuación, el precio de un activo particular se denota como ![]() . El proceso de Itô que describe su evolución a través del tiempo está dado por:
. El proceso de Itô que describe su evolución a través del tiempo está dado por:






Para ilustrar el efecto cambiario en las economías analizadas provocado por la decisión de los electores en el Reino Unido en cuanto a su salida en la Unión Europea, se considera el precio del dólar estadounidense con respecto de la moneda de cada uno de los siguientes países: Australia, Canadá, República Checa, Dinamarca, China (Hong Kong), Japón, México, Noruega, Polonia, Rusia, Singapur, Sudáfrica, Suecia, Suiza, Turquía, Reino Unido y los países correspondientes a la Zona Euro tenidos en cuenta como un único país.
Los datos que se utilizan fueron tomados desde el 27 de junio de 2013 hasta el 27 de julio de 2016 y obtenidos de World Integrated Trade Solution, software desarrollado por el Banco Mundial en colaboración con la Conferencia de las Naciones Unidas sobre Comercio y Desarrollo (UNCTAD por sus siglas en inglés). Los parámetros de la ecuación diferencial que describe el comportamiento del activo en cada región fueron estimados, a partir de la serie de precios diarios, de la siguiente manera: la tendencia fue calculada como el promedio de los rendimientos diarios durante los últimos 3 años y la volatilidad como la desviación estándar de dichos rendimientos. En la Tabla 1 se muestran los resultados de las estimaciones.
Tabla 1
Promedio y desviación estándar de las rentabilidades diarias del precio del dólar estadounidense
en términos de la moneda local de cada uno de las regiones consideradas.
Prom. Rent. |
Desv. Est. Rent. |
|
Australia |
0,03% |
0,67% |
Canada |
0,03% |
0,51% |
Czech Republic |
0,03% |
0,62% |
Denmark |
0,02% |
0,56% |
Hong Kong, China |
0,00% |
0,03% |
Japan |
0,01% |
0,60% |
Mexico |
0,05% |
0,69% |
Norway |
0,05% |
0,73% |
Poland |
0,03% |
0,68% |
Russian Federation |
0,10% |
1,51% |
Singapore |
0,01% |
0,35% |
South Africa |
0,05% |
0,94% |
Sweden |
0,03% |
0,63% |
Switzerland |
0,01% |
0,79% |
Turkey |
0,06% |
0,76% |
United Kingdom |
0,02% |
0,60% |
Zona Euro |
0,02% |
0,56% |
Fuente: Cálculos propios a partir de información de Forex Capital Markets.
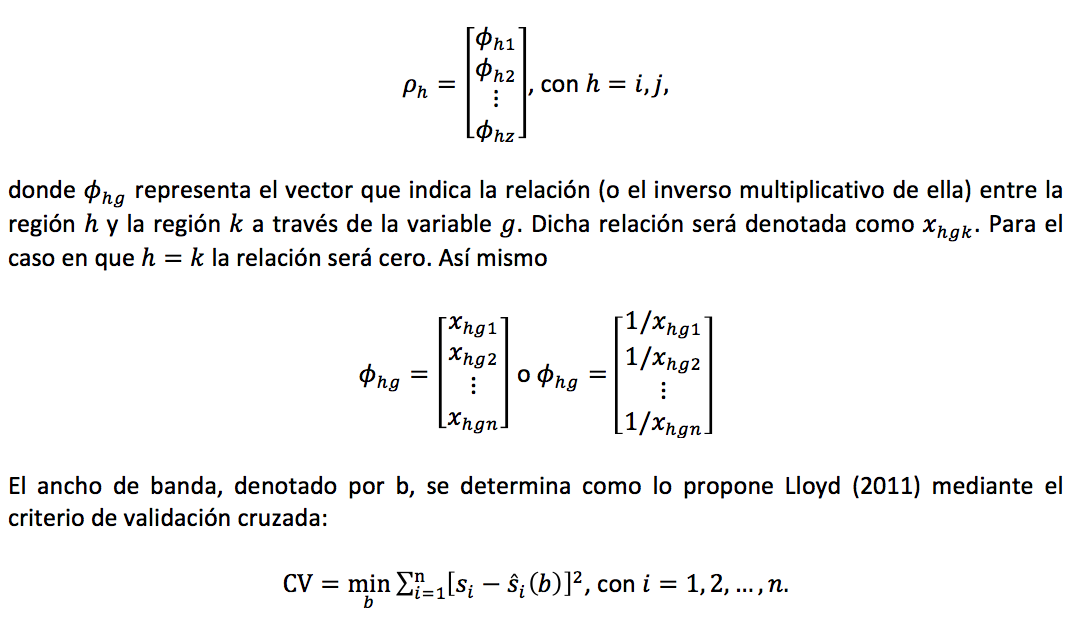
Para el cálculo de la matriz de ponderaciones se utilizó la distancia euclidiana entre las regiones analizadas, y como indicador de la relación entre cada pareja de regiones la diferencia de las exportaciones y las importaciones entre ellas (flujo comercial) medidas en miles de dólares. Los datos se detallan en el Anexo 1. Al utilizar sólo el flujo comercial como la variable que define la posición relativa de cada región, el vector ![]() será entonces de dimensión ph, el cual es representado en forma de columnas la Tabla 2.
será entonces de dimensión ph, el cual es representado en forma de columnas la Tabla 2.
Tabla 2
Vectores (columnas) que definen la posición relativa de cada región analizada.
Australia |
Canada |
Czech Republic |
Denmark |
Hong Kong, China |
Japan |
|
Australia |
0,0000 |
6,0504 |
2,2211 |
1,4886 |
-4,0426 |
-0,0455 |
Canada |
6,0504 |
0,0000 |
9,7900 |
31,3519 |
-12,5554 |
-0,6763 |
Czech Republic |
2,2211 |
9,7900 |
0,0000 |
-1,3475 |
1,4605 |
2,6978 |
Denmark |
1,4886 |
31,3519 |
-1,3475 |
0,0000 |
-1,8835 |
-0,7084 |
Hong Kong, China |
-4,0426 |
-12,5554 |
1,4605 |
-1,8835 |
0,0000 |
0,0302 |
Japan |
-0,0455 |
-0,6763 |
2,6978 |
-0,7084 |
0,0302 |
0,0000 |
Mexico |
2,2136 |
1,6728 |
-1,0354 |
-3,2323 |
1,9464 |
-0,0697 |
Norway |
4,4536 |
-1,2291 |
-1,5972 |
-1,9409 |
9,1579 |
-2,3288 |
Poland |
4,1822 |
1,1431 |
0,1581 |
1,1689 |
3,1639 |
-0,4899 |
Russian Federation |
-2,1151 |
-2,7523 |
-2,1648 |
1,0522 |
1,7144 |
0,1314 |
Singapore |
0,1209 |
-2,7811 |
5,7805 |
-4,5512 |
0,0270 |
-0,2964 |
South Africa |
-4,0414 |
20,0606 |
-2,7284 |
-5,8790 |
0,9417 |
1,7189 |
Sweden |
0,9054 |
1,4875 |
-1,0243 |
-0,9013 |
-1,8404 |
1,7040 |
Switzerland |
0,5017 |
0,3811 |
-1,1818 |
8,6270 |
0,0442 |
0,2959 |
Turkey |
-42,5405 |
-3,8698 |
-0,6898 |
10,4823 |
3,7875 |
-0,3565 |
United Kingdom |
0,3445 |
-0,2065 |
-0,2254 |
-0,5673 |
0,1384 |
-0,2771 |
Zona Euro |
0,6005 |
0,7707 |
-0,5619 |
1,2562 |
0,8912 |
3,3503 |
Mexico |
Norway |
Poland |
Russian Federation |
Singapore |
South Africa |
|
Australia |
2,2136 |
4,4536 |
4,1822 |
-2,1151 |
0,1209 |
-4,0414 |
Canada |
1,6728 |
-1,2291 |
1,1431 |
-2,7523 |
-2,7811 |
20,0606 |
Czech Republic |
-1,0354 |
-1,5972 |
0,1581 |
-2,1648 |
5,7805 |
-2,7284 |
Denmark |
-3,2323 |
-1,9409 |
1,1689 |
1,0522 |
-4,5512 |
-5,8790 |
Hong Kong, China |
1,9464 |
9,1579 |
3,1639 |
1,7144 |
0,0270 |
0,9417 |
Japan |
-0,0697 |
-2,3288 |
-0,4899 |
0,1314 |
-0,2964 |
1,7189 |
Mexico |
0,0000 |
-11,4757 |
8,5348 |
2,5200 |
-2,0621 |
-2,5716 |
Norway |
-11,4757 |
0,0000 |
3,1635 |
7,9914 |
-0,9347 |
-196,1169 |
Poland |
8,5348 |
3,1635 |
0,0000 |
0,1762 |
-4,8331 |
-2,2035 |
Russian Federation |
2,5200 |
7,9914 |
0,1762 |
0,0000 |
-0,2112 |
-8,1181 |
Singapore |
-2,0621 |
-0,9347 |
-4,8331 |
-0,2112 |
0,0000 |
-1,1873 |
South Africa |
-2,5716 |
-196,1169 |
-2,2035 |
-8,1181 |
-1,1873 |
0,0000 |
Sweden |
1,8332 |
0,3592 |
-1,9327 |
-0,3517 |
1,8106 |
1,5952 |
Switzerland |
-3,8951 |
2,1440 |
2,5103 |
1,3167 |
0,1669 |
-0,6758 |
Turkey |
-1,9357 |
-4,9139 |
-1,5426 |
-0,0595 |
14,8666 |
-2,3290 |
United Kingdom |
-5,1648 |
-0,0627 |
-0,1447 |
-0,3562 |
0,2213 |
-0,3942 |
Zona Euro |
0,8470 |
-0,6392 |
0,5422 |
-0,3610 |
1,7121 |
1,8138 |
Sweden |
Switzerland |
Turkey |
United Kingdom |
Zona Euro |
|
Australia |
0,9054 |
0,5017 |
-42,5405 |
0,3445 |
0,6005 |
Canada |
1,4875 |
0,3811 |
-3,8698 |
-0,2065 |
0,7707 |
Czech Republic |
-1,0243 |
-1,1818 |
-0,6898 |
-0,2254 |
-0,5619 |
Denmark |
-0,9013 |
8,6270 |
10,4823 |
-0,5673 |
1,2562 |
Hong Kong, China |
-1,8404 |
0,0442 |
3,7875 |
0,1384 |
0,8912 |
Japan |
1,7040 |
0,2959 |
-0,3565 |
-0,2771 |
3,3503 |
Mexico |
1,8332 |
-3,8951 |
-1,9357 |
-5,1648 |
0,8470 |
Norway |
0,3592 |
2,1440 |
-4,9139 |
-0,0627 |
-0,6392 |
Poland |
-1,9327 |
2,5103 |
-1,5426 |
-0,1447 |
0,5422 |
Russian Federation |
-0,3517 |
1,3167 |
-0,0595 |
-0,3562 |
-0,3610 |
Singapore |
1,8106 |
0,1669 |
14,8666 |
0,2213 |
1,7121 |
South Africa |
1,5952 |
-0,6758 |
-2,3290 |
-0,3942 |
1,8138 |
Sweden |
0,0000 |
-8,1260 |
-2,5254 |
-0,2680 |
0,5578 |
Switzerland |
-8,1260 |
0,0000 |
0,3095 |
0,0365 |
0,3435 |
Turkey |
-2,5254 |
0,3095 |
0,0000 |
-0,1764 |
0,6563 |
United Kingdom |
-0,2680 |
0,0365 |
-0,1764 |
0,0000 |
0,1135 |
Zona Euro |
0,5578 |
0,3435 |
0,6563 |
0,1135 |
0,0000 |
Fuente: Cálculos propios.
A partir de la posición relativa de cada región es posible calcular la distancia euclidiana entre ellas, la cual se muestra en la Tabla 3, y estimar las coordenadas respectivas mostradas en la Gráfica 1.
Tabla 3
Distancia euclidiana entre las regiones analizadas.
Australia |
Canada |
Czech Republic |
Denmark |
Hong Kong, China |
Japan |
|
Australia |
- |
36,6 |
4,9 |
2,2 |
16,3 |
0,0 |
Canada |
36,6 |
- |
14,7 |
20,8 |
101,9 |
37,2 |
Czech Republic |
4,9 |
14,7 |
- |
0,5 |
39,2 |
5,1 |
Denmark |
2,2 |
20,8 |
0,5 |
- |
30,6 |
2,4 |
Hong Kong, China |
16,3 |
101,9 |
39,2 |
30,6 |
- |
16,0 |
Japan |
0,0 |
37,2 |
5,1 |
2,4 |
16,0 |
- |
Mexico |
4,9 |
14,7 |
0,0 |
0,5 |
39,1 |
5,1 |
Norway |
19,8 |
2,5 |
5,0 |
8,8 |
72,2 |
20,2 |
Poland |
17,5 |
3,5 |
3,8 |
7,3 |
67,6 |
17,9 |
Russian Federation |
4,5 |
66,7 |
18,8 |
13,0 |
3,7 |
4,3 |
Singapore |
0,0 |
35,2 |
4,4 |
1,9 |
17,3 |
0,0 |
South Africa |
16,3 |
101,8 |
39,2 |
30,6 |
0,0 |
16,0 |
Sweden |
0,8 |
26,5 |
1,7 |
0,3 |
24,5 |
0,9 |
Switzerland |
0,3 |
30,8 |
3,0 |
1,0 |
20,7 |
0,3 |
Turkey |
1.809,7 |
2.361,1 |
2.003,6 |
1.938,6 |
1.482,1 |
1.805,8 |
United Kingdom |
0,1 |
32,6 |
3,5 |
1,3 |
19,2 |
0,2 |
Zona Euro |
0,4 |
29,7 |
2,6 |
0,8 |
21,6 |
0,4 |
Mexico |
Norway |
Poland |
Russian Federation |
Singapore |
South Africa |
|
Australia |
4,9 |
19,8 |
17,5 |
4,5 |
0,0 |
16,3 |
Canada |
14,7 |
2,5 |
3,5 |
66,7 |
35,2 |
101,8 |
Czech Republic |
0,0 |
5,0 |
3,8 |
18,8 |
4,4 |
39,2 |
Denmark |
0,5 |
8,8 |
7,3 |
13,0 |
1,9 |
30,6 |
Hong Kong, China |
39,1 |
72,2 |
67,6 |
3,7 |
17,3 |
0,0 |
Japan |
5,1 |
20,2 |
17,9 |
4,3 |
0,0 |
16,0 |
Mexico |
- |
5,0 |
3,9 |
18,7 |
4,4 |
39,1 |
Norway |
5,0 |
- |
0,1 |
43,1 |
18,8 |
72,2 |
Poland |
3,9 |
0,1 |
- |
39,7 |
16,5 |
67,6 |
Russian Federation |
18,7 |
43,1 |
39,7 |
- |
5,0 |
3,7 |
Singapore |
4,4 |
18,8 |
16,5 |
5,0 |
- |
17,3 |
South Africa |
39,1 |
72,2 |
67,6 |
3,7 |
17,3 |
- |
Sweden |
1,7 |
12,6 |
10,7 |
9,1 |
0,6 |
24,5 |
Switzerland |
2,9 |
15,6 |
13,5 |
6,8 |
0,1 |
20,6 |
Turkey |
2.002,9 |
2.208,4 |
2.183,0 |
1.634,2 |
1.820,0 |
1.482,2 |
United Kingdom |
3,5 |
16,9 |
14,7 |
6,0 |
0,0 |
19,2 |
Zona Euro |
2,6 |
14,8 |
12,8 |
7,4 |
0,2 |
21,5 |
Sweden |
Switzerland |
Turkey |
United Kingdom |
Zona Euro |
|
Australia |
0,8 |
0,3 |
1.809,7 |
0,1 |
0,4 |
Canada |
26,5 |
30,8 |
2.361,1 |
32,6 |
29,7 |
Czech Republic |
1,7 |
3,0 |
2.003,6 |
3,5 |
2,6 |
Denmark |
0,3 |
1,0 |
1.938,6 |
1,3 |
0,8 |
Hong Kong, China |
24,5 |
20,7 |
1.482,1 |
19,2 |
21,6 |
Japan |
0,9 |
0,3 |
1.805,8 |
0,2 |
0,4 |
Mexico |
1,7 |
2,9 |
2.002,9 |
3,5 |
2,6 |
Norway |
12,6 |
15,6 |
2.208,4 |
16,9 |
14,8 |
Poland |
10,7 |
13,5 |
2.183,0 |
14,7 |
12,8 |
Russian Federation |
9,1 |
6,8 |
1.634,2 |
6,0 |
7,4 |
Singapore |
0,6 |
0,1 |
1.820,0 |
0,0 |
0,2 |
South Africa |
24,5 |
20,6 |
1.482,2 |
19,2 |
21,5 |
Sweden |
- |
0,2 |
1.887,5 |
0,3 |
0,1 |
Switzerland |
0,2 |
- |
1.852,6 |
0,0 |
0,0 |
Turkey |
1.887,5 |
1.852,6 |
- |
1.839,1 |
1.861,1 |
United Kingdom |
0,3 |
0,0 |
1.839,1 |
- |
0,1 |
Zona Euro |
0,1 |
0,0 |
1.861,1 |
0,1 |
- |
Fuente: Cálculos propios.
Gráfica 1. Coordenadas y posición relativa de las regiones analizadas.

Fuente: Cálculos propios realizados mediante análisis factorial.
Tabla 4
Precios del dólar estadounidense expresados en términos de la
moneda local en cada región al 27 de julio de 2016.
Australia |
1,3329 |
Canada |
1,3188 |
Czech Republic |
24,599 |
Denmark |
6,771 |
Hong Kong, China |
7,7571 |
Japan |
104,66 |
Mexico |
18,7755 |
Norway |
8,568 |
Poland |
3,9722 |
Russian Federation |
65,9448 |
Singapore |
1,3586 |
South Africa |
14,355 |
Sweden |
8,6595 |
Switzerland |
0,9924 |
Turkey |
3,0453 |
United Kingdom |
0,7615 |
Zona Euro |
0,9101 |
Fuente: Cálculos propios.
De acuerdo con los precios de la divisa estadounidense presentados en la Tabla 4 y el cálculo de los parámetros de tendencia y volatilidad, las matrices del modelo serán:


Los estimadores de ![]() encontrados indican la parte del cambio promedio en el precio del dólar estadounidense en cada región, que es explicada por el precio de ese activo en las regiones vecinas en términos económicos. Los estimadores de
encontrados indican la parte del cambio promedio en el precio del dólar estadounidense en cada región, que es explicada por el precio de ese activo en las regiones vecinas en términos económicos. Los estimadores de ![]() indican la parte de la desviación estándar del cambio que explican dichas regiones.
indican la parte de la desviación estándar del cambio que explican dichas regiones.
El ancho de banda óptimo para la regresión económicamente ponderada que explica la variabilidad en la tendencia y en la volatilidad es 165,3. Los errores estimados para cada región se presentan en la Tabla 5.
Tabla 5
Errores estimados para cada región.
Región |
µ estimado |
ν estimado |
Australia |
-0,001221451 |
-0,001118979 |
Canada |
-0,001222648 |
-0,003583121 |
Czech Republic |
-0,002729845 |
-0,054036392 |
Denmark |
-0,001936932 |
-0,017927371 |
Hong Kong, China |
-0,003827447 |
-0,062160687 |
Japan |
-0,025564701 |
-0,255717615 |
Mexico |
0,001584831 |
-0,027920746 |
Norway |
-7,66483E-05 |
-0,008456891 |
Poland |
-0,001511134 |
-0,005341221 |
Russian Federation |
0,041942146 |
0,443605976 |
Singapore |
-0,001494613 |
-0,005499805 |
South Africa |
0,001147789 |
0,015492559 |
Sweden |
-0,001221075 |
-0,017010853 |
Switzerland |
-0,001401547 |
0,00070398 |
Turkey |
0 |
0 |
United Kingdom |
-0,001261224 |
-0,000636968 |
Zona Euro |
-0,001259735 |
-0,0013463 |
Fuente: Cálculos propios.
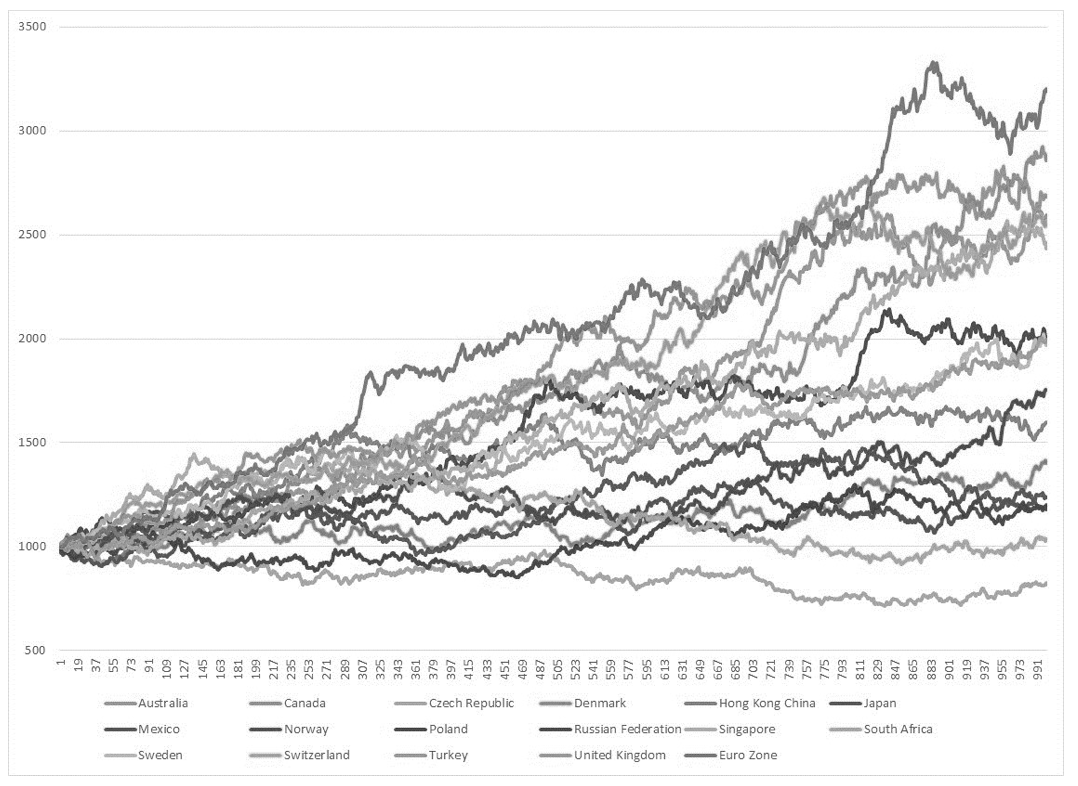
En la Gráfica 2 se muestra una simulación para el precio de la divisa estadounidense (base 1000) en términos de la moneda local de cada una de las regiones de la muestra.
Gráfica 2.
Simulación del precio de la divisa estadounidense (base 1.000) en términos de la moneda local.
Fuente: Cálculos propios a partir de información de Forex Capital Markets.
Para establecer una comparación entre el escenario inicial y uno simulado, se supuso que la salida del Reino Unido de la Unión Europea supondrá una disminución del 20% en el flujo comercial entre ese país y la Zona Euro; así mismo, se supuso que el comercio con Noruega y Suiza se incrementará en un 15%, pues como se detalla en Perrett (2016), Noruega le proveería al Reino Unido acceso libre de tarifas al mercado único europeo y Suiza, aunque no comercia con dicho mercado, tiene múltiples tratados de libre comercio con países de la Unión Europea. Posteriormente se realizaron 10.000 simulaciones, extrayendo al final el precio promedio de la divisa estadounidense en cada uno de los países. La repercusión que se tendría en el precio de la divisa estadounidense en cada una de las regiones se muestra en la Gráfica 3.
Gráfica 3. Resultado de la simulación del precio del dólar estadounidense en términos de la moneda local.
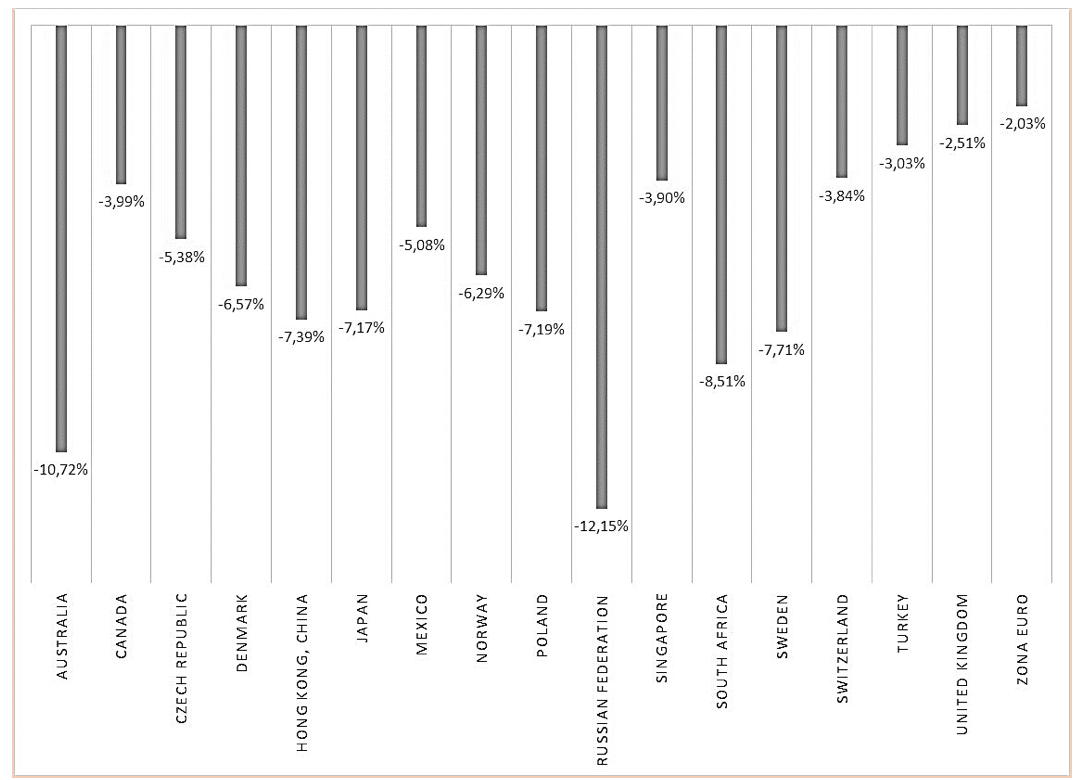
Fuente: Cálculos propios a partir de información de Forex Capital Markets.
Los resultados presentados en la Gráfica 3 muestran que la variación supuesta en el flujo comercial del Reino Unido, supondría en un período de cuatro años una apreciación de las monedas locales de los países considerados en la muestra, con respecto a su comportamiento sin Brexit, especialmente del rublo (12,15%) y el dólar australiano (10,72%). Contrario a lo esperado, el euro y la libra esterlina no sufrirían gran variación ante ese escenario (apreciación del 2,03% y 2,51% respectivamente).
Se consideró una divisa negociada en 17 mercados, cuyo precio en cada uno de ellos es modelado por medio de un Proceso de Itô que incluye la posible interrelación entre los precios, modelada mediante econometría espacial, donde la distancia entre las regiones se mide en términos económicos y financieros y no geográficos. Al poder analizar de forma integrada la dinámica del precio del activo en cada región, es posible simular el comportamiento del activo en cada región y los efectos que un cambio en los precios o en las relaciones económicas de una región en particular tendría sobre las demás.
Las regiones que se utiliza como muestra para modelar el precio relativo del dólar con respecto de monedas locales son: Australia, Canadá, República Checa, Dinamarca, China (Hong Kong), Japón, México, Noruega, Polonia, Rusia, Singapur, Sudáfrica, Suecia, Suiza, Turquía, Reino Unido y la Zona Euro.
Los hallazgos empíricos muestran que una disminución del 20% en el flujo comercial entre el Reino Unido y la Zona Euro y un aumento del 15% entre el primero y sus socios más cercanos, Noruega y Suiza, supondría en un período de cuatro años, en comparación con su comportamiento sin Brexit, una apreciación de las monedas locales de los países considerados en la muestra, especialmente del rublo (12,15%) y el dólar australiano (10,72%). Contrario a lo esperado, el euro y la libra esterlina no sufrirían gran variación ante ese escenario (apreciación del 2,03% y 2,51%, respectivamente).
Investigaciones futuras sobre el tema pueden tratar sobre la distancia económica óptima que debe existir entre un país o región y sus vecinos de tal forma que se minimice el efecto sobre el precio de un activo en particular ante un choque externo, tal como el supuesto en la Sección 3. Estas investigaciones pueden ayudar a calcular los efectos colaterales de imponer sanciones económicas a un país, determinar el sistema de compensaciones a países aliados como lo propone Coase (1960) en el contexto empresarial, o incluso aportar elementos para determinar la relación costo – beneficio de estas medidas.
En la Tabla 6 se relaciona el valor del flujo comercial que tuvieron los siguientes países en el año 2015: Australia, Canadá, República Checa, Dinamarca, China (Hong Kong), Japón, México, Noruega, Polonia, Rusia, Singapur, Sudáfrica, Suecia, Suiza, Turquía, Reino Unido y los países correspondientes a la zona euro considerados como un único país. Los valores se encuentran expresados en millones de dólares estadounidenses y corresponden a la balanza comercial entre los países de la muestra.
Tabla 6
Flujo comercial entre las regiones.
Australia |
Canada |
Czech Republic |
Denmark |
Hong Kong, China |
Japan |
|
Australia |
- |
165.279 |
450.225 |
671.752 |
- 247.363 |
- 21.989.542 |
Canada |
165.279 |
- |
102.145 |
31.896 |
- 79.647 |
- 1.478.711 |
Czech Republic |
450.225 |
102.145 |
- |
- 742.136 |
684.697 |
370.668 |
Denmark |
671.752 |
31.896 |
- 742.136 |
- |
- 530.937 |
- 1.411.705 |
Hong Kong, China |
- 247.363 |
- 79.647 |
684.697 |
- 530.937 |
- |
33.128.615 |
Japan |
- 21.989.542 |
- 1.478.711 |
370.668 |
- 1.411.705 |
33.128.615 |
- |
Mexico |
451.750 |
597.792 |
- 965.819 |
- 309.376 |
513.770 |
- 14.351.286 |
Norway |
224.537 |
- 813.575 |
- 626.100 |
- 515.222 |
109.195 |
- 429.412 |
Poland |
239.109 |
874.843 |
6.325.563 |
855.526 |
316.064 |
- 2.041.293 |
Russian Federation |
- 472.801 |
- 363.338 |
- 461.935 |
950.421 |
583.283 |
7.607.795 |
Singapore |
8.270.782 |
- 359.568 |
172.994 |
- 219.721 |
37.025.678 |
- 3.373.841 |
South Africa |
- 247.438 |
49.849 |
- 366.515 |
- 170.098 |
1.061.901 |
581.766 |
Sweden |
1.104.543 |
672.279 |
- 976.309 |
- 1.109.471 |
- 543.371 |
586.865 |
Switzerland |
1.993.335 |
2.623.850 |
- 846.135 |
115.915 |
22.622.452 |
3.378.960 |
Turkey |
- 23.507 |
- 258.408 |
- 1.449.702 |
95.399 |
264.023 |
- 2.805.441 |
United Kingdom |
2.902.950 |
- 4.843.435 |
- 4.436.195 |
- 1.762.807 |
7.225.847 |
- 3.609.150 |
Zona Euro |
1.665.287 |
1.297.520 |
- 1.779.664 |
796.021 |
1.122.106 |
298.480 |
Mexico |
Norway |
Poland |
Russian Federation |
Singapore |
South Africa |
|
Australia |
451.750 |
224.537 |
239.109 |
- 472.801 |
8.270.782 |
- 247.438 |
Canada |
597.792 |
- 813.575 |
874.843 |
- 363.338 |
- 359.568 |
49.849 |
Czech Republic |
- 965.819 |
- 626.100 |
6.325.563 |
- 461.935 |
172.994 |
- 366.515 |
Denmark |
- 309.376 |
- 515.222 |
855.526 |
950.421 |
- 219.721 |
- 170.098 |
Hong Kong, China |
513.770 |
109.195 |
316.064 |
583.283 |
37.025.678 |
1.061.901 |
Japan |
- 14.351.286 |
- 429.412 |
- 2.041.293 |
7.607.795 |
- 3.373.841 |
581.766 |
Mexico |
- |
- 87.141 |
117.168 |
396.822 |
- 484.952 |
- 388.857 |
Norway |
- 87.141 |
- |
316.110 |
125.135 |
- 1.069.810 |
- 5.099 |
Poland |
117.168 |
316.110 |
- |
5.673.827 |
- 206.907 |
- 453.831 |
Russian Federation |
396.822 |
125.135 |
5.673.827 |
- |
- 4.735.091 |
- 123.182 |
Singapore |
- 484.952 |
- 1.069.810 |
- 206.907 |
- 4.735.091 |
- |
- 842.238 |
South Africa |
- 388.857 |
- 5.099 |
- 453.831 |
- 123.182 |
- 842.238 |
- |
Sweden |
545.486 |
2.784.241 |
- 517.409 |
- 2.843.018 |
552.309 |
626.897 |
Switzerland |
- 256.734 |
466.408 |
398.364 |
759.467 |
5.992.110 |
- 1.479.689 |
Turkey |
- 516.616 |
- 203.505 |
- 648.262 |
- 16.810.342 |
67.265 |
- 429.374 |
United Kingdom |
- 193.619 |
- 13.867.575 |
- 6.909.669 |
- 2.807.781 |
4.519.458 |
- 2.536.536 |
Zona Euro |
1.180.614 |
- 1.564.437 |
1.844.221 |
- 2.770.236 |
584.093 |
551.320 |
Sweden |
Switzerland |
Turkey |
United Kingdom |
Zona Euro |
|
Australia |
1.104.543 |
1.993.335 |
- 23.507 |
2.902.950 |
1.665.287 |
Canada |
672.279 |
2.623.850 |
- 258.408 |
- 4.843.435 |
1.297.520 |
Czech Republic |
- 976.309 |
- 846.135 |
- 1.449.702 |
- 4.436.195 |
- 1.779.664 |
Denmark |
- 1.109.471 |
115.915 |
95.399 |
- 1.762.807 |
796.021 |
Hong Kong, China |
- 543.371 |
22.622.452 |
264.023 |
7.225.847 |
1.122.106 |
Japan |
586.865 |
3.378.960 |
- 2.805.441 |
- 3.609.150 |
298.480 |
Mexico |
545.486 |
- 256.734 |
- 516.616 |
- 193.619 |
1.180.614 |
Norway |
2.784.241 |
466.408 |
- 203.505 |
- 13.867.575 |
- 1.564.437 |
Poland |
- 517.409 |
398.364 |
- 648.262 |
- 6.909.669 |
1.844.221 |
Russian Federation |
- 2.843.018 |
759.467 |
- 16.810.342 |
- 2.807.781 |
- 2.770.236 |
Singapore |
552.309 |
5.992.110 |
67.265 |
4.519.458 |
584.093 |
South Africa |
626.897 |
- 1.479.689 |
- 429.374 |
- 2.536.536 |
551.320 |
Sweden |
- |
- 123.062 |
- 395.981 |
- 3.730.793 |
1.792.641 |
Switzerland |
- 123.062 |
- |
3.231.203 |
23.796.202 |
2.911.228 |
Turkey |
- 395.981 |
3.231.203 |
- |
- 5.669.207 |
1.523.635 |
United Kingdom |
- 3.730.793 |
23.796.202 |
- 5.669.207 |
- |
11.017.046 |
Zona Euro |
1.792.641 |
2.911.228 |
1.523.635 |
11.017.046 |
- |
Fuente: The World Bank y United Nations Conference on Trade and Development (UNCTAD).
Agudelo, J. E. (2011). Incidencia de la estación del metro en San Javier en los precios de las viviendas de la zona. Lincoln Institute of Land Policy; Universidad EAFIT. 2011, pp 17-19.
Ali, L. and Kestens (2006). Contagion and Crises Clusters: Toward a Regional Warning System? Journal Review of World Economics. Vol. 142, No. 4, pp 814-839.
Ali, L., Lebreton, M (2013) The Fall of Bretton Woods: which Geography Matters? Economics Bulletin. Vol. 2, No. 1, pp. 1396-1419.
Banco Central Europeo, B. (06 de 09 de 2016). EUROSISTEMA. Obtenido de El Euro: https://www.ecb.europa.eu/euro/changeover/2002/html/index.es.html.
Barrett, A., Bergin, A., FitzGerald, J., Lambert, D., McCoy, D., Morgenroth, E., . . . Studnicka, Z. (2015). Scoping the Possible Economic Implications of Brexit on Ireland. Dublin, Ireland: The Economic and Social Research Institute.
Black, F. and M. Scholes (1973). The Pricing of Option and Corporative Liabilities. Journal of Political Economy, Vol. 81, No 3, pp. 637-654.
Boulanger, p., & Philippidis, G. (2015). The End of a Romance? A Note on the Quantitative Impacts of a "Brexit" from the EU. Journal of Agricultural Economics, Vol. 66, 3., pp 832-842.
Breinlich, H., Dhingra, S., Estrin, S., Huang, H., Ottaviano, G., Sampson, T., . . . Wadsworth, J. (2016). BREXIT 2016 Policy analysis from the Centre for Economic Performance. London: Centre for Economic Performance.
Chasco-Yrigoyen, C. (2003). Econometría espacial aplicada a la predicción-extrapolación de datos micro territoriales. Tesis doctoral.
Coase, R. H. (1960). The problem of social cost. In Classic Papers in Natural Resource Economics (pp. 87-137). Palgrave Macmillan, UK.
Cox, J. J. Ingersolly S. Ross (1985b). A theory of the term structure of interest rates, Econometrica, Vol. 53, No. 2, pp. 385-467.
Cox, J., J. Ingersoll y S. Ross(1985a).An Intertemporal General Equilibrium Model of Asset Prices, Econometrica, Vol. 53, No. 2, pp. 385-467.
Diario Oficial de la Unión Europea (DOUE), DO C 326 de 26.10.2012. Versión consolidada del Tratado de la Unión Europea. (T. V.-D. FINALES, Entrevistador)
EUR-Lex. (07 de 09 de 2016). EUR-Lex. Obtenido de El acceso al Derecho de la Unión europea: http://eur-lex.europa.eu/collection/eu-law/treaties-accession.html#new-2-9
Fotheringham S., Brunsdon C., and Charlton M. (2002). Geographically Weighted Regression: The Analysis of Spatially Varying Relationships. John Wiley & Sons, Chichester.
Geary, R. C. (1954). The Contiguity Ratio and Statistical Mapping. Journal of the Royal Statistical Society, Vol. 5, No. 3, pp. 115-145.
Grinols, E. L. y S. J. Turnovsky (1993). Risk, the Financial Market, and Macroeconomic Equilibrium, Journal of Economic Dynamics and Control, Vol. 17, No. 1-2, pp. 1-36.
Howell, J. (27 de 06 de 2016). BBC NEWS. Obtenido de Three effects of Brexit on the City of London: http://www.bbc.com/news/business-36625894
Lash, H. (22 de 08 de 2016). Business. Obtenido de New York topples London from property pinnacle as Brexit deters foreign investors: http://www.thenational.ae/business/property/new-york-topples-london-from-property-pinnacle-as-brexit-deters-foreign-investors.
Lee, M. y W. Li (2005). Drift and Diffusion Function Specification for Short-Term Interest Rates, Economic Letters, Vol. 86, No. 3, pp. 339-346.
Lloyd, Christopher D. (2011). Local Models for Spatial Analysis. 2nd ed. CRC Press. U.S.A.
Longstaff, F. A. (1989). A Nonlinear General Equilibrium Model of the Term Structure of Interest Rates, Journal of Financial Economics, Vol. 23, No. 2, pp. 195-224.
Merton, R. C. (1973). Theory of Rational Option Pricing. Bell Journal of Economics, Vol. 4, No. 1, pp. 141-183.
Möller, A., & Oliver, T. (2014). The United Kingdom and the European Union: what would a “Brexit” mean for the EU and other States around the World? European and global perspectives. The United Kingdom: DGAPanalyse.
Morán, P. (1948). The Interpretation of Statistical Maps. Journal of the Royal Statistical Society, No. 10, 243-251.
Mur L., J. (1999). Heterocedasticidad y Autocorrelación espacial: una propuesta de identificación de series espaciales. Estadística Española, Vol. 41, No. 144, pp. 79-104.
Paelinck, J. H. P. y Klaassen, L. H., (1979). Spatial Econometrics. Saxon House Farnborough. Kiel Institute for World Economics.
Perrett, M. (2016). Five trade options for life after brexit: AHDB. Food Manufacture, 2016July Retrieved from www.scopus.com.
Schmedders, K. (1998). Computing Equilibria in the General Equilibrium Model with Incomplete Asset Markets. Journal of Economic Dynamics and Control, Vol. 22, No. 8-9, pp. 1375-1401.
Turnovsky, S. J. (1986). Short-Term and Long-Term Interest Rates in a Monetary Model of a Small Open Economy. Journal of International Economics, Vol. 20, No. 3-4, pp. 291-311.
UE, U. E. (30 de 03 de 2010). Diario Oficial de la Uión Europea, DOUE. Maastricht, Limburgo, Holanda.
Van, R. J. (2016). BREXIT 2016 Policy analysis from the Centre for Economic Performance. London: Centre for Economic Performance.
Vasicek, O. (1977). An Equilibrium Characterization of the Term Structure. Journal of Financial Economics, Vol. 5, No. 2, pp. 177-188.
Venegas-Martínez, F. (2001). Temporary Stabilization: a Stochastic Analysis. Journal of Economic Dynamics and Control, Vol. 25, No. 9, pp. 1429-1449.
Venegas-Martínez, F. (2006a). Stochastic Temporary Stabilization: Undiversifiable Devaluation and Income Risks. Economic Modelling, Vol. 23, No. 1, pp. 157-173.
Venegas-Martínez, F. (2006b). Fiscal Policy in a Stochastic Temporary Stabilization Model: Undiversifiable Devaluation Risk, Journal of World Economic Review, Vol. 1, No. 1, pp. 87-106.
Venegas-Martínez, F. (2008). Riesgos financieros y económicos, productos derivados y decisiones económicas bajo incertidumbre, 2da. Edición, Cengage Learning, México.
Venegas-Martínez, F. y B. González-Aréchiga (2002). Cobertura de tasas de interés con futuros del mercado mexicano de derivados: un modelo estocástico de duración y convexidad. El Trimestre Económico, Vol. 59(2) No. 274, pp. 227-250.
Wallace, T. (06 de 09 de 2016). The Telegraph. Obtenido de London's million-pound homes hit hardest by Brexit: http://www.telegraph.co.uk/business/2016/09/06/londons-million-pound-homes-hit-hardest-by-brexit/
Weiler, J. (2015). Brexit: No Happy Endings. European journal of international law, Vol. 26, No. 1215, pp 1-7.
1. Instituto Tecnológico Metropolitano, Medellín, Colombia. Email: albertoagudelo@itm.edu.co
2. Instituto Tecnológico Metropolitano, Medellín, Colombia. Email: luisfranco@itm.edu.co
3. Instituto Tecnológico Metropolitano, Medellín, Colombia. Email: luisefranco@itm.edu.co
4. Universidad de las Américas Puebla, Cholula, México. Email: nora.gavira@udlap.mx