

 Vol. 38 (Nº 55) Año 2017. Pág. 31
Vol. 38 (Nº 55) Año 2017. Pág. 31
Ivanovnna Milqueya CRUZ Pichardo 1; Angel PUENTES Puente 2; Julio CABERO Almenara 3
Recibido: 13/08/2017 • Aprobado: 05/09/2017
RESUMEN: Una de las estrategias de enseñanza aprendizaje más importante en la actualidad es la resolución de problemas. El uso de las redes sociales en la resolución de problemas es una de las problemáticas que en estos últimos tiempos está siendo abordada con gran interés y preocupación por la investigación educativa ya que se crean ambientes que propician aprendizaje y mejora el rendimiento de los alumnos participantes en la experiencia formativa. |
ABSTRACT: One of the most important teaching strategies today is problem solving. The use of social networks in the resolution of problems is one of the problems that in recent times is being approached with great interest and concern for educational research as it creates environments that promote learning and improves the performance of students participating in the formative experience. |
La resolución de problemas matemáticos se ha convertido en uno de los grandes retos con los que se enfrentan los docentes del área de las matemáticas, debido a su importancia como estrategia de enseñanza aprendizaje y al papel que estos juegan en crear las conexiones con otras áreas del saber.
A pesar de su importancia y formar parte de la mayoría de los planes de estudio, no posee un rol activo en la enseñanza no universitaria y es un problema que se da de forma más significativa en las aulas iberoamericanas. La mayoría de nuestras aulas se centran en el proceso de conceptualización y procedimientos, dejando de lado su aplicación. Se fundamentan en la trasmisión y reproducción de conocimiento (presentación del ejercicio, explicación y trabajo individual), donde el docente es el responsable de construir el conocimiento para el estudiante, anticipándose a su razonamiento y convirtiéndolo en agente pasivo de su proceso de aprendizaje.
Esto genera la necesidad de buscar un modelo que les permita a los estudiantes desarrollar las competencias necesarias, para su desempeño académico como laboral, que puedan identificar y entender el papel que juega las matemáticas en el mundo actual (OECD, 2004) y les permita resolver problemas colectivamente intercambiando y exponiendo sus ideas.
Por lo anterior, se ha propuesto realizar el presente estudio, en atención a la necesidad de crear una estrategia de aprendizaje de las matemáticas basada en la resolución de problemas y la colaboración mediante el uso de las redes sociales (RS), como espacio de discusión y reflexión; es decir, se propone crear un espacio de enseñanza que desarrolle la comprensión de los conceptos y destrezas matemáticas, que no esté orientada solamente a enseñar métodos para resolver problemas.
Las RS se han convertido en un fenómeno de nuestros tiempos, “T2O Media” en su informe del 2012 sobre “Social Media” reveló que como cada dos horas hay 5 millones de estados nuevos en Facebook, 340 millones de Tweets al día, y donde Google + tiene 250 millones de usuarios registrados. A su vez “iLifebelt”, en su informe del 2016 sobre Redes sociales en Centroamérica y el Caribe, reveló que el 38.5% pasa más de 3 horas al día usando las redes sociales y que el 42.3% de esos usuarios de las redes sociales son estudiantes no universitarios. Respecto a su penetración en el terreno educativo, diferentes Informes Horizon ponen de manifiesto (García, Peña, Johnson, Smith, Levine y Haywood, 2010; Durall, Gros, Maina, Johnson y Adams, 2012) el fuerte impacto que está teniendo, tanto a nivel universitario, como no universitario.
Respecto a su conceptualización, se reconocen perspectivas diferentes al definirlas: las que se centran en la comunicación y colaboración como variables fundamentales y las que se basan en el estudio de las características estructurales de sus herramientas (Cabero, Barroso, Llorente y Marín, 2013). A su vez, De Haro (2011) las define como una estructura social que se puede representar mediante nodos conectados por aristas, donde los nodos representan a los individuos y las aristas las relaciones establecidas.
También se debe tener en cuenta que existen diferentes tipos: verticales-horizontales, profesionales-ocio, abiertas-cerradas, gratuitas-de pago, libres-alojadas en servidores propios.
Y por lo que se refiere a sus posibilidades educativas y unificando las propuestas de diferentes autores (Camacho, 2010; De Haro, 2011; Romero, 2011; Joosten, 2012; Cabero y Marín, 2013; Cruz, 2016) se pueden señalar las siguientes: permiten la creación de una inteligencia colectiva, amplían las fronteras del proceso de enseñanza aprendizaje, facilitan la comunicación, favorecen la construcción colaborativa del conocimiento, implican un cambio en la gestión de los procesos de enseñanza, fomentan una visión compartida del conocimiento, favorecen la socialización del grupo, constituyen un espacio de encuentro entre los diferentes actores del proceso enseñanza aprendizaje, permiten centralizar en un único sitio todas las actividades docentes, aumentan la fluidez y sencillez de la comunicación entre profesores y alumnos, facilitan la coordinación y trabajo de diversos grupos de aprendizaje, aumentan la interacción entre profesores y alumnos, facilitan la retroalimentación de los estudiantes a tiempo, mejora el aprendizaje.
Respecto a sus inconvenientes se pueden señalar los siguientes: tener precaución con la privacidad, su incorporación exige del profesorado crear actividades motivadoras para que no se conviertan en un distractor y elemento lúdico y de ocio, la falta de formación de los padres en estos aspectos podría traer desconfianza y poco control al momento de usarlas en casa, y el riesgo del acoso cibernético. (Roig, 2011; Aydin, 2012).
Su utilización implica que el docente desempeñe nuevos roles, que superen la mera transmisión de contenidos, y alcance otros como los de guía, dinamizador y orientador. Minocha, Schroeder y Schneider (2011) hablan de cuatro roles fundamentales que el profesor puede desempeñar con el uso de los software sociales: pedagógico (facilita el aprendizaje a través de actividades interactivas, la reflexión crítica y la retroalimentación en línea), social (facilita la creación y el crecimiento de una comunidad estudiantil en línea a través de una comunicación frecuente y positiva), de dirección (guía en el procedimiento, en la organización y la administración de las tareas a ejecutar) y técnica (proporciona apoyo técnico).
A la hora de la selección de la RS a utilizar, Joosten (2012) sugiere que se deben establecer criterios que permitan lograr aprendizajes significativos en los estudiantes y que sea eficiente en su uso, acceso y costo. Llorente (2012) por su parte propone que la red seleccionada esté basada en los principios del trabajo colaborativo y que permita incorporar la diversidad de elementos multimedia disponibles para lograr los objetivos educativos.
Para el estudio se seleccionó la red “Edmodo” (https://www.edmodo.com/?language=es), por ser un servicio cerrado, que permite el envío de mensajes de texto, adjuntar archivos, corregir actividades y prácticas, así como trabajar con alumnos de todas las edades, inclusive con menores de 14 años. Además, se puede tener contacto continuo con los alumnos, lo que facilita un apoyo sistemático de las clases presenciales. (De Haro, 2011).
Edmodo fue creada en el año 2008 por Jeff O'Hara y Nic Borg, y por sus características constituye una buena herramienta para la educación, por lo que está siendo utilizada para el desarrollo de diferentes experiencias educativas (Holland y Muilenburg, 2011; Sáez, Lorraine, y Yoshiro, 2013; Vázquez, 2013; Alonso, Morte, y Almansa, 2015).
Edmodo se caracteriza por ser una red privada, segura y gratuita, y ha sido especialmente diseñada para favorecer la interacción y la colaboración entre docentes y estudiantes. Cuenta con diferentes roles: profesores, alumnos, padres, administración de la escuela, lo que permite la interacción entre los diferentes integrantes de la comunidad educativa. Al momento del registro se especifica el rol que se ejercerá dentro de la red.
En este estudio, se les solicitó a los padres, que se le creara una figura en Edmodo, para que observaran lo realizado por los estudiantes, pues en el imaginario social siguen percibiéndose las redes como tecnologías asociadas a los lúdico y ocioso.
Una de las grandes ventajas de esta plataforma educativa y red social, es que no exige instalación ni configuración, su registro y matriculación se realiza en la web, mediante un código enviado por el docente a sus alumnos, con el que pueden acceder a su curso.
De acuerdo con De Haro (2011) se reconoce que la plataforma permite realizar las siguientes actividades:
• Cambiar el nombre del grupo.
• Establecer todos los nuevos miembros de estado de "sólo lectura"
• Activar/desactivar la moderación en el grupo.
• Cambiar el grupo de nivel designado de grado y la materia.
• Archivo del grupo: al final del curso, semestre o año, es posible que se desee guardar los grupos. Esto hace que quede inactivo, pero aún se permite ver todas las comunicaciones del mismo.
• Eliminar el grupo; se tiene la opción de eliminar el grupo y todo su contenido de forma definitiva.
Tanto el estudiante como el profesor comparten el “muro” como herramienta central de comunicación, permitiendo que interactúen en este espacio.
En la Investigación realizada por Sáez, Lorraine, Yoshiro (2013) respecto al uso de Edmodo en proyectos colaborativos internacionales para educación primaria, se encontraron conclusiones interesantes sobre el grado de aceptación de esta RS por los docentes, que son las siguientes:
• La actitud de los docentes hacia el uso del Edmodo fue positiva y consideran que es una herramienta adecuada y eficaz en los contextos educativos.
• Manifiestan numerosas ventajas de comunicación y actividades colaborativas.
• Resaltan la seguridad del entorno
• Se mejora la organización de la clase y se fomentan cambios en el proceso de enseñanza aprendizaje
• Los recursos para docentes y las comunidades aportan materiales y actividades de fácil acceso para los estudiantes.
Por otra parte, se indica que son diversas las estrategias grupales a utilizar en las RS: método de la solución de problemas, método de proyectos individuales, método del caso, método del contrato, investigación grupal, observación tríadica, seminario, coloquio, simulación didáctica, y ponencia científica (Chávez, Solís, e Iriarte, 2012). Mostrándose verdaderamente eficaz la incorporación de estrategias colaborativas (Gray, Vitak, Easton y Ellison, 2013).
Para finalizar se destacan dos aspectos: primero, que los alumnos muestran altos niveles de satisfacción cuando se utilizan en la enseñanza y adquieren con ellas niveles significativos de aprendizaje (Aydin, 2012; Irwin, Ball, Desbrow y Leveritt, 2012; Cabero y Marín, 2013; Greenhow y Gleason, 2014; Becerra y Martín, 2015; Güler, 2015; Cruz, 2016) y segundo, que se han llevado a cabo más estudios y reflexiones teóricas que investigaciones (Veletsianos y Navarrete, 2012; López, Vásquez, y Sánchez-Serrano, 2015), y estas además son muy escasas en el terreno de las matemáticas.
No estaría mal reconocer desde el principio que las matemáticas se conciben como un lenguaje, nos provee de un sistema de significados, combina el lenguaje ordinario con el vocabulario técnico y ayuda a interpretar las definiciones, los símbolos, las notaciones, los modelos, los cuadros, los gráficos, los diagramas, las reglas y los procedimientos. Su enseñanza podríamos suscribirlas en dos grandes corrientes: los que proponen el desarrollo de la competencia matemática como finalidad de su enseñanza y los que persiguen la construcción del conocimiento matemático como base de la organización curricular; aunque para algunos autores (Goñi, 2011) ambos enfoques son complementarios.
En el sistema de la República Dominicana (RD), que es donde se realizó la investigación, la enseñanza de las matemáticas se fundamenta en un enfoque por competencias. Entendiendo por competencia matemática: “la capacidad que tiene un individuo de identificar y comprender el papel que desempeñan las matemáticas en el mundo, emitir juicios bien fundados y utilizar e implicarse en las matemáticas de una manera que satisfaga sus necesidades vitales como un ciudadano constructivo, comprometido y reflexivo… hace referencia a la capacidad que tienen los alumnos para analizar, razonar y comunicarse eficazmente cuando plantean, formulan, resuelven e interpretan problemas matemáticos en diversas situaciones”. (OECD, 2004).
En definitiva, la competencia matemática es la capacidad para plantear, formular, resolver, e interpretar problemas utilizando las matemáticas dentro de una variedad de situaciones y contextos. Ella se hace realidad y tiene sentido cuando, los elementos y razonamientos matemáticos son utilizados para enfrentar situaciones en la vida cotidiana. Por lo que su desarrollo se alcanzaría en la medida en que los conocimientos matemáticos se apliquen de manera espontánea en cualquier situación, no solo en el campo de las matemáticas sino en otros terrenos de conocimientos y en la vida cotidiana. Y en este sentido el proyecto PISA (OECD, 2003) estructura la competencia matemática en grandes bloques: cantidad, espacio y forma, cambios, relaciones e incertidumbre y resolución de problemas.
Respecto a la última, que es en la que se centrará la presente investigación y se incluyen aspectos relacionados con: traducir las situaciones reales o esquemas o modelos matemáticos; plantear, formular y definir diferentes tipos de problemas (matemáticos, aplicados, de respuesta abierta, cerrados,…); resolver diferentes tipos de problemas seleccionando las estrategias adecuadas y comprobando las soluciones propuestas.
Para evaluar el nivel de competencia matemática del alumnado se han efectuado diferentes propuestas, entre las que se incluyen las ocho competencias planteadas por el proyecto PISA/OCDE y en las que se centrará este trabajo: pensar matemáticamente (PR), plantear y resolver problemas matemáticos (PRP), modelar matemáticamente (MO), argumentar matemáticamente (ARG), representar entidades matemáticas (situaciones y objetos) (REP), utilizar los símbolos matemáticos (REP), comunicarse con las matemáticas y comunicar sobre matemáticas (CO), y utilizar ayudas y herramientas (incluyendo las nuevas tecnologías) (REP). Las cuatro primeras se pueden agrupar dentro de la categoría “habilidades para resolver cuestiones en matemáticas”, y las cuatro últimas en “habilidades para usar el lenguaje y herramientas matemáticas” (OECD, 2003).
Además de los enfoques por competencias, es importante conocer los principios y estándares que ha establecido el Consejo Nacional de Profesores de Matemática (NCTM, 2003) ya que estos constituyen un eje importante en el currículo dominicano y en el Internacional. Sus estándares que son los siguientes: igualdad, currículum, enseñanza, aprendizaje, evaluación y tecnología. Estos estándares, que de acuerdo con Rico y Lupiánez (2008, 274) pueden ser de contenidos y procesos. Los de contenidos se refieren a: números y operaciones¸ álgebra, geometría, medida, y análisis de datos y probabilidad; mientras que los de proceso hacen referencia a: resolución de problemas, razonamiento y demostración, comunicación, conexiones, y representación.
Por lo que se refiere al currículo de “Matemática de Educación Secundaria” de la República Dominicana, que es el contexto en el cual se desarrolla esta experiencia, se enmarca en la Propuesta Curricular del Plan Decenal, y se fundamenta en la visión de las matemáticas en constante evolución, con problemas por resolver, en la que se valora tanto el producto de la actividad matemática, como el proceso que conlleva.
En dicha propuesta curricular se destacan: la solución de problemas, el desarrollo de competencias de comunicación y de pensamiento crítico, reflexivo y sistemático. Esta visión de la enseñanza de la matemática se concreta en el desarrollo de siete ejes: Conocimiento, Comunicación, Razonamiento Matemático, Conexiones, Resolución de Problemas, Toma de Decisiones y Valoración de la Matemática.
En ellos, la resolución de problemas matemáticos juega un papel importante y su rol debería ser más activo en la enseñanza de los grados no universitarios, ya que les permite a los alumnos emplear los conceptos y destrezas matemáticas que han aprendido (Jiménez y Verschaffel, 2014), permitiéndoles practicar hechos matemáticos, reglas, principios y operaciones, así como la comprensión y el razonamiento (Ilany y Margolin, 2010).
Para Monroy (2014) al hablar de resolución de problemas matemáticos se debe tener claro qué es un problema y las características que deben tener para que no sean problemas rutinarios, sino interesantes para la enseñanza. Y en este sentido Bejarano y Lirio (2010), mencionan que deben poseer las siguientes características:
a) llevar a los alumnos a tomar decisiones o hacer juicios basados en hechos, información lógica y fundamentada,
b) es necesaria la cooperación de los integrantes del grupo de trabajo para abordar el problema de manera eficiente,
c) las preguntas deben ser abiertas, ligadas a un aprendizaje previo, es decir dentro de un marco de conocimiento específicos-temas de controversia; y
d) el contenido de los objetivos del curso deben ser incorporados en el diseño de los problemas.
Los problemas, para que sean significativos deben cumplir las siguientes exigencias: la existencia de un interés, la no existencia de una solución inmediata, la presencia de diversos caminos o métodos de solución, la atención por parte de una persona para llevar acabo un conjunto de acciones, y tendientes a resolver esta tarea; es decir, un problema está, hasta que existe un interés y se emprenden acciones específicas para intentar resolverlo (Santos, 2010).
Por otra parte, el problema seleccionado o diseñado, debe permitir que se resuelva de manera colaborativa, que admita aportaciones individuales y que no tenga una solución cerrada. (Bejarano y Lirio, 2010). Y al mismo tiempo que provoque que los alumnos utilicen sus conocimientos previos, ya que en este proceso los alumnos serán capaces de aplicar el pensamiento sistémico para resolver las nuevas situaciones que se le presentarán a lo largo de su vida.
Respecto a los criterios a considerar para la construcción de un problema Bejarano y Lirio (2010) presentan los siguientes: que estimulen el pensamiento, análisis y razonamiento, asumir el aprendizaje autorregulado, utilizar el conocimiento previo, proponer un contexto realista, permitir descubrir los objetivos de aprendizaje, activar la curiosidad, elegir tópicos relacionados con el área del conocimiento para el que se forma, asegurar contextos amplios, y elegir un vocabulario apropiado.
Para Jonassen (2011) los problemas son de diversos tipos: inducción de reglas, toma de decisiones, diagnóstico, rendimiento estratégico, implementación, diseño, y dilema. Su selección debe ser planeada y estructurada de tal manera que permita la solución con diferentes propuestas o alternativas. Mientras que Ramírez, Gómez y Sánchez (2010) establecen que al momento de crear o seleccionar un problema, se debe tener presente las siguientes características: que involucren el interés de los alumnos y motiven su aprendizaje; que los estudiantes desarrollen una línea de razonamiento que esté cimentada en evidencias; sean suficientemente complejos como para motivar la participación de un grupo de alumno y no únicamente a uno de ellos; que no sean demasiado estructurados y más bien con un final abierto, que permita la participación de todos los estudiantes, así como varias posibles legítimas soluciones o varios caminos hacia una sola solución; e incorporen los objetivos de aprendizaje de un curso.
Por último indicar, que deben estar diseñados para motivar al estudiante a la búsqueda independiente de la información a través de los diferentes medios que tenga disponible, y deben estimular el uso de los conocimientos previos, que les propiciará “aprender a aprender”.
El problema de investigación planteado consistió en analizar la posibilidad que ofrecen las RS para desarrollar el aprendizaje de las matemáticas, mediante de la resolución de problemas, mediante la participación de los alumnos, con el objetivo de medir su rendimiento académico.
Con el interés de facilitar la comprensión de la investigación realizada, a continuación se relacionan todos los objetivos que permiten concretar el problema de investigación:
Las fases de la investigación y las actividades realizadas en ellas se presentan a continuación en la figura 1.
Figura 1
Fases del diseño de la investigación

La experiencia se realizó durante el curso académico 2014-2015, en un colegio bilingüe privado, ubicado en una zona céntrica de la ciudad de Santo Domingo. La muestra seleccionada correspondió a 50 estudiantes que cursaban la asignatura de geometría en décimo grado, con edades comprendidas entre los 14 a 17 años. Siendo la mayoría de 15 (f=13, 26,0%) y 16 años (f=32, 64,0%). El 58,0% (f=29) eran mujeres y el 42,0% (f= 21) hombres. La duración de la experiencia fue de dos meses.
El tipo de muestreo que se utilizó fue causal, que como señala Sabariego (2012) se basa en la facilidad de acceso por parte del investigador a los individuos objeto de estudio, también considerado de conveniencia, fortuito o accidental, por el cual el investigador selecciona los casos que están más disponibles (Alaminos, 2006).
Se seleccionó el colegio bilingüe como muestra de la investigación, ya que disponía de los medios y recursos tecnológicos requeridos para este tipo de estudio, lo que no es usual en todos los centros educativos de la República Dominicana, contando con la autorización de la dirección del centro y de los padres de los estudiantes para aplicar la investigación.
Es necesario señalar que se tomaron en cuenta los planteamientos realizados por Tejedor y García-Valcácel (2007), que establecen “el rendimiento académico implica calificaciones, tasas de éxito/fracaso que pueden ser individual o colectivo, actitudes y satisfacción los cuales pueden ser medidos mediante pruebas orales o escritas”. Elemetos que han sido utilizados en diferentes estudios, como el de Barroso y Cabero, que se analizaron la capacidad de mejorar el rendimiento académico de los alumnos mediante la utilización de diseños y formas específicas de utilización de tecnologías, entendiendo por rendimiento la capacidad de conocimiento, comprensión y aplicación de la información presentadas por la tecnologías concreta utilizada, (Barroso y Cabero, 2010).
Para la construcción de la prueba se utilizaron los siguientes criterios:
Para la construcción tanto de pretest, como del postest se seleccionaron 25 preguntas. En la tabla 1, a continuación, se presentan las competencias que se pretendían alcanzar y el número de preguntas formuladas tanto en el pretest como postest.
Tabla 1
Relación clúster, estándares y número de preguntas del Instrumento de Rendimiento.
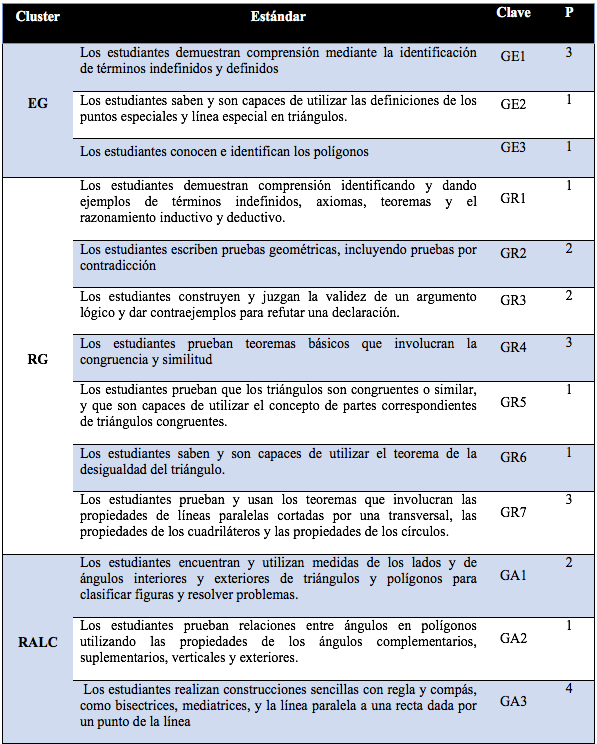
Para tener una mejor comprensión de los resultados alcanzados en el estudio, en primer lugar, se presentaran los obtenidos de manera general por todos los alumnos, para después presentar las alcanzadas en cada clúster de objetivos de aprendizaje. El análisis sería repetido para conocer si la variable género repercutía en los resultados alcanzados. Los análisis estadísticos se efectuaron con el programa SPSS V.20 bajo Windows.
Las hipótesis analizadas fueron las siguientes:
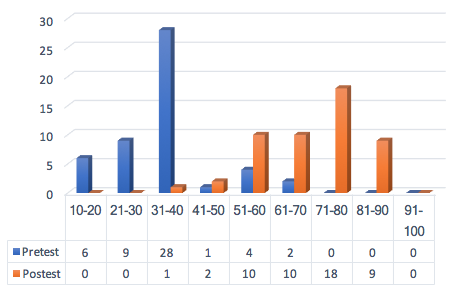
Como se señaló anteriormente, las pruebas constaban de 25 ítems a los que les dio un valor de 4 puntos para un total de 100 puntos. El valor mínimo para aprobar la asignatura para este grado es de 70 puntos, y si se observa las medias del pretest de 35.44 y del postest de 70.24 y se comparan con el gráfico de la figura 2, se observa que para la primera etapa de la experiencia de formación ningún alumno aprobó el examen, lo que fue lógico, ya que los alumnos no habían recibido ninguna formación al respecto, mientras que después de la experiencia formativa el 54% (f=27) aprobaron la prueba.
Figura 2
Frecuencia de las calificaciones de instrumento de rendimiento
Para saber si existían diferencias significativas desde un punto de vista estadístico se aplicó el test de Wilcoxon, alcanzando las puntuaciones presentadas a continuación, en la tabla 2.
Tabla 2
Prueba de rangos con signos de Wilcoxon del análisis de rendimiento
(Nota: a. Postest < Pretest; b. Postest > Pretest; c. Postest = Pretest).
|
N |
Rango Promedio |
Suma de Rangos |
|
Postest – Pretest |
Rangos Negativos |
0a |
.00 |
.00 |
Rangos Positivos |
50b |
25.50 |
1275.00 |
|
Empates |
0c |
|
|
|
Total |
50 |
|
|
|
Al observar la tabla de signos se aprecia que los rangos son positivos y por lo tanto es posible asumir la condición Postest > Pretest; lo que quiere decir que hubo cambios positivos después de la experiencia formativa. Al mismo tiempo señalar que el valor Z de -6,169 significativa a 0,000, permitían rechazar la H0, y en consecuencia se señala que hubo cambios significativos en los resultados en cuanto a la adquisición de información a corto plazo por parte de los estudiantes.
A continuación, se presentan los resultados alcanzados respecto a los diferentes clústeres propuestos: EG, RG, y RALC.
Lo que respecta a “EG”, los valores alcanzados en la Prueba de los Rangos con signos de Wilcoxon se presentan en la tabla 3.
Yabla 3
Prueba de rangos con signos de Wilcoxon del análisis de Explorando Geometría.
|
N |
Rango Promedio |
Suma de Rangos |
|
Postest - Pretest. Explorando Geometría
|
Rangos Negativos |
0 |
.00 |
.00 |
Rangos Positivos |
50 |
25.50 |
1275.00 |
|
Empates |
0 |
|
|
|
Total |
50 |
|
|
|
Valores que aportan un valor Z=-6.583, significativo a alfa =0.000. Puntuación que permite rechazar la H0 y aceptar la H1, con un riesgo alfa de equivocación inferior al 0.05.
Por lo que se refiere a “RG”, los valores alcanzados se presentan en la tabla 4.
Tabla 4
Prueba de rangos con signos de Wilcoxon del análisis de razonamiento geométrico.
|
N |
Rango Promedio |
Suma de Rangos |
|
Postest - Pretest Razonamiento Geométrico |
Rangos Negativos |
0 |
.00 |
.00 |
Rangos Positivos |
50 |
25.50 |
1275.00 |
|
Empates |
0 |
|
|
|
Total |
50 |
|
|
|
Prueba que aporta un valor de Z=-6.199, con un valor significativo igual al 0.000, valor que permite rechazar la H0 y aceptar, con riesgo alfa a equivocación inferior a 0.05, la H1.
Los valores alcanzados en “RALC” se presentan en la tabla 5.
Tabla 5
Prueba de rangos con signos de Wilcoxon del análisis de relación de ángulos
|
N |
Rango Promedio |
Suma de Rangos |
|
Postest - Pretest Relación de ángulos, líneas y construcciones |
Rangos Negativos |
0 |
.00 |
.00 |
Rangos Positivos |
50 |
25.50 |
1275.00 |
|
Empates |
0 |
|
|
|
Total |
50 |
|
|
|
En este caso, los valores muestran un Z=-6.209 con un valor significativo igual al 0.000; lo que permite aceptar la H1.
Para analizar si había diferencias significativas en función del género de los estudiantes, se formularon las siguientes hipótesis:
H0 (Hipótesis Nula): No existen diferencias significativas entre el género y a la adquisición de información a corto plazo tras haber participado en la experiencia de formación basada en las redes sociales y la resolución de problemas, con un riesgo alfa de 0.05 de equivocación.
H1 (Hipótesis Alternativa): Existen diferencias significativas entre el género y a la adquisición de información a corto plazo tras haber participado en la experiencia de formación basada en las redes sociales y la resolución de problemas, con un riesgo alfa de 0.05 de equivocación.
Para su contraste se aplicó la U Mann-Whitney. Alcanzando los valores presentados en la tabla 6.
Tabla 6
Prueba de rangos con signo de U Mann-Whitney para rendimiento general.
|
Sexo |
N |
Rango Promedio |
Suma de Rangos |
Pretest |
Femenino |
29 |
21.52 |
624.00 |
Masculino |
21 |
31.00 |
651.00 |
|
Total |
50 |
|
|
|
Postest |
Femenino |
29 |
23.10 |
670.00 |
Masculino |
21 |
28.81 |
605.00 |
|
Total |
50 |
|
|
Al analizar la tabla 7, se puede comprobar que los niveles de significación obtenidos en el caso del pretest fueron de 0.022, que al comienzo de la experiencia formativa, eran inferiores al nivel de significación de 0.05, lo que mostraba que existían diferencias significativas entre los géneros; luego de la experiencia formativa se obtuvo un nivel de significancia de 0.169, el cual fue superior al nivel adoptado para aceptar o rechazar una hipótesis, por lo que evidencia que luego de la experiencia formativa se debe asumir H0, referida a la no existencia de diferencias en función del género de los alumnos.
Tabla 7
Estadísticos de contraste de rendimiento general.
Estadísticos de Contraste |
||
|
Pretest |
Postest |
Mann-Whitney U |
189.000 |
235.000 |
Z |
-2.299 |
-1.375 |
Asymp. Sig. |
.022 |
.169 |
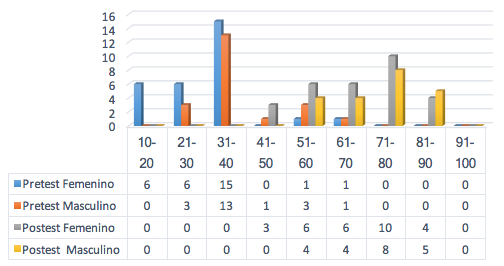
La distribución de las notas según el género, se puede observar a continuación, en la figura 3, donde se puede observar que antes de la experiencia formativa existía una tendencia, en los estudiantes de ambos sexos, a no “aprobar” la prueba; ahora bien, después de la experiencia formativa del uso de las redes sociales para la resolución de problemas matemáticos, el 48% (f=14) de las hembras y el 62% (f=13) de los varones, aprobaron el examen con una calificación mayor de 71 puntos. Lo que indica que a pesar de que no se observan diferencias significativas en el postest entre los géneros, el porcentaje de los estudiantes varones que aprobó el examen era superior al de las hembras.
Figura 3
Frecuencia rendimiento general y género
Las diferencias en cuanto a los clústeres de objetivos y el género, alcanzando con la prueba de Mann-Whitney, fueron analizados, cuyos resultados se señalan en la siguiente tabla 8:
Figura 8
Estadístico de contraste de diferentes aspectos de la prueba de rendimiento
|
EG |
RG |
RALC |
|||
|
Pretest |
Posttest |
Pretest |
Postest |
Pretest |
Postest |
Mann-Whitney U |
250.000 |
255.000 |
203.000 |
212.000 |
274.500 |
292.000 |
Z |
-1.253 |
-1.157 |
-2.054 |
-1.834 |
-.660 |
-.254 |
Asymp. Sig. (2-tailed) |
.210 |
.247 |
.040 |
.067 |
.509 |
.800 |
Se puede apreciar que en los casos de “EG” y “RALC” no existen diferencias relevantes, ya que el nivel de significación, en ambas etapas de la experiencia formativa, era mayor que el establecido de 0.05; por lo tanto, se asume como cierta la H0 que indica que no existen diferencias de género en cuanto a la adquisición de conocimiento a corto plazo de los objetivos relacionados con “EG” y “RALC”
Ahora bien, en cuanto a “RG” ante de la experiencia formativa el nivel de significancia era de 0.04, el cual es menor al nivel establecido para rechazar o aprobar la hipótesis por lo que se puede asumir como verdadera la H1 antes de la experiencia formativa. Después de la experiencia formativa, el nivel de significancia es de 0.067, el cual es mayor que el establecido, por lo tanto no se presenta diferencias significativas y se puede asumir como cierta la H0.
El estudio realizado confirma el planteamiento de que las redes sociales pueden ser utilizadas, siguiendo una metodología colaborativa, para mejorar el rendimiento académico alcanzado por los alumnos en la resolución de problemas matemáticos, y es independiente al género de los estudiantes, logrando eliminar las diferencias existentes al comienzo del estudio.
La elaboración de objetos de aprendizaje en diferentes soportes, textuales y videográficos, el trabajo individual inicial de los alumnos con dichos materiales, y la interacción entre los alumnos para resolver en la red social los diferentes problemas matemáticos que se le propusieron permite reconocer que la estrategia utilizada por el docente para propiciar la interacción de los estudiantes con las RS ha sido eficaz para el aprendizaje de los contenidos y capacidades que se perseguía que los estudiantes alcanzaran, así como para el aprendizaje del funcionamiento de EDMODO.
Los resultados de significatividad obtenidos se han mostrado tanto para el rendimiento general, como para el que conformaba los diferentes clústeres propuestos: EG, RG, y RALC.
La red EDMODO, utilizada en el estudio se mostró accesible y robusta para las diferentes actividades académicas desarrolladas, desde la ubicación de archivos en diferentes soportes al seguimiento de trabajo de los estudiantes planteados. Se debe señalar que el aprendizaje por parte de los estudiantes de su funcionamiento y de las posibilidades que ofrece, fue bastante rápido y amigable, no habiéndose encontrado ningún obstáculo con ninguno de los estudiantes que participaron en la experiencia.
La experiencia fue valorada de forma positiva por los padres de los hijos, y no hubo ninguna crítica respecto a la estrategia y metodología empleada.
El trabajo realizado permite aseverar que en un área tan abstracta como las matemáticas, las redes sociales utilizadas como base para el trabajo colaborativo, se muestran también eficaces en esta disciplina, también mostraba un alto nivel de satisfacción de los alumnos hacia esta estrategia de enseñanza (Cruz, 2016).
El presente estudio es consistente con investigaciones realizadas sobre las posibilidades que ofrecen las redes sociales de manera general para el aprendizaje de los estudiantes, como las de: (Aydin, 2012; Irwin, Ball, Desbrow y Leveritt, 2012; Cabero y Marín, 2013; Greenhow y Gleason, 2014; Güler, 2015), y de manera particular las referentes a la utilización de la red EDMODO para ser aplicada en contextos no universitarios de (Holland y Muilenburg, 2011; Sáez, Lorraine, y Yoshiro, 2013; Vázquez, 2013).
Alaminos, A. (2006). El muestreo en la investigación social. En Antonio Alaminos y Juan Luis. Castejón. Elaboración, análisis e interpretación de encuestas, cuestionarios y escalas de opinión (pp. 46-67). Alcoy: Marfil.
Alonso, S., Morte, E. y Almansa, S., (2015). Redes sociales aplicadas a la educación: EDMODO. EDMETIC: Revista de Educación Mediática y TIC, 4(2), pp. 88-111.
Aydin, S. (2012). A review of research on Facebook as an educational environment. Education Technology Research Development, 60(6), 1093-1106.
Barroso, J., y Cabero, J. (2010). La investigación en TIC. Madrid: Síntesis.
Becerra, M. y Martín, F. (2015). Visión de las plataformas virtuales de enseñanza y las redes sociales por los usuarios estudiantes. Pixel-Bit. Revista de Medios y Educación, 47, pp. 223-230.
Bejarano, M. y Lirio, J. (2010). La utilización de problemas auténticos en la enseñanza superior. En A. Escribano, y Á. Del Valle, El Aprendizaje Basado en Problemas (ABP). Una Propuesta metodológica en Educación Superior (pp. 37-53). Madrid: Narcea.
Cabero, J. y Marín, V. (2013). Percepciones de los estudiantes universitarios latinoamericanos sobre las redes sociales y el trabajo en grupo. RUSC. Universities and Knowledge Society Journal, 10(2), pp. 219-235.
Cabero, J., Barroso, J., Llorente, M, y Marín, V. (2013). Las Redes Sociales como instrumento para la formación: Percepciones de los alumnos universitarios hacia el trabajo en grupo. Sevilla: Grupo de Investigación Didáctica-Universidad de Sevilla.
Camacho, M. (2010). Las redes sociales para enseñar y aprender. Reflexiones pedagógicas básicas. En Linda. Castañeda, Aprendizajes con redes sociales. Tejidos educativos para los nuevos entornos (pp. 91-104). Sevilla: Eduforma.
Chávez, M., Solis, N., e Iriarte, A. (2012). Estrategias de Aprendizaje Colaborativo para Redes Sociales Digitales. XX Encuentro Internacional de Educación a Distancia: Redes y alianza más allá de las modalidades educativas. Jalisco, México: UDG Virtual.
Cruz, I. (2016). Percepciones en el uso de las redes sociales y su aplicación en la enseñanza de las matemáticas. Pixel-Bit. Revista de Medios y Educación. 48, pp. 165-186.
De Haro, J. (2011). Redes Sociales para la educación. Madrid: Anaya.
Durall, E., Gros, B., Maina, M., Johnson, L., y Adams, S. (2012). Perspectivas tecnológicas: educación superior en Iberoamérica 2012-2017. Austin, Texas: The New Media Consortium.
Garcia, I., Peña, I., Johnson, L., Smith, R., Levine, A., y Haywood, K. (2010). Informe Horizon: Edición Iberoamericana 2010. Austin, Texas: The new Media Consortium.
Goñi, J. M. (2011). Didácticas de las Matemáticas. Barcelona: Grao.
Gray, R., Vitak, J. Easton, E. y Ellison, N. (2013). Examining social adjustment to college in the age of social media: Factors influencing successful transitions and persistence. Computers & Education, 67, pp. 193–207.
Greenhow, CH. y Gleason, B. (2014). Social scholarship: Reconsidering scholarly practices in the age of social media. British Journal of Educational Technology, 45(3), pp. 392–402.
Güler, K. (2015). Social media-based learning in the design studio: A comparative study. Computers & Education, 87, pp. 192-203.
Holland, C. y Muilenburg, L. (2011). Supporting Student Collaboration: Edmodo in the Classroom. In M. Koehler & P. Mishra (Eds.), Proceedings of Society for Information Technology & Teacher Education International Conference 2011 (pp. 3232-3236). Chesapeake, VA: AACE. En http://www.editlib.org/p/36816 Recuperado el 20/09/2013.
Ilany, B., y Margolin, B. (2010). Language and mathematics: Bridging between natural language and mathematical language in solving problems in mathematics. Creative Education, pp. 138-148.
ILifebelt (2016). Estudios de redes sociales en Centroamérica y el Caribe. En http://ilifebelt.com/6to-estudio-anual-ilifebelt-redes-sociales-centroamerica-caribe-2016/2016/08/. Recuperado el 18/03/2017
Irwin, C., Ball, L., Desbrow, B., y Leveritt, M. (2012). Students' perceptions of using Facebook as an interactive learning resource at university. Australasian Journal of Educational Technology, 28(7), pp. 1221-1232.
Jonassen, D. (2011). Supporting problem solving in PBL. Journal of problem based learning, 5(2), pp. 95-119.
Joosten, T. (2012). Social Media for Educators. Strategies and best practices. California: Jossey-Bass.
Llorente, M. (2012). Educar a través de la red. Evolución y aspectos educativos a tener en cuenta. En E. Navas, Web 2.0 Innovación e investigación educativa (pp. 93-115). Caracas: Universidad Metropolitana.
López, E., Vásquez, E., y Sánchez-Serrano, J. (2015). Estudio bibliométrico de Pixel-bit, revista de medios y educación (2000-2013). Pixel-Bit. Revista de Medios y Educación, 46, pp. 65-85.
Minocha, S., Schroeder, A., y Schneider, C. (2011). Role of the educator in social software initiatives in further and higher education: A conceptualization and research agenda. British Journal of Educational Technology, 42, (6), pp. 889-903.
Monroy, J. (2014). La resolución de problemas matemáticos y su impacto en el pensamiento crítico de Ciudadano. Revista de Cooperación.com, pp. 81-85.
NCTM. (2003). Principios y Estándares para la Educación Matemática. Sevilla: Sociedad Andaluza de Educación Matemática Thales.
OECD. (2003). The PISA 2003 assessment framework. Mathematics, reading, science and problem solving knowledge and skills. Paris: OECD.
Ramírez, M., Gómez, G., y Sánchez, A. (2010). Estudio Bilateral México – EUA de las Técnicas de enseñanza aprendizaje en el Nivel Superior. Cuadernos de Educación y Desarrollo, 2. Recuperado de: http://www.eumed.net/rev/ced/17/mfrn.htm (20/05/2014).
Rico, L., y Lupiánez, J. (2008). Competencias Matemáticas desde una perspectiva curricular. Madrid: Alianza.
Roig, R. (2011). Redes Sociales educativas. Propuestas para la intervención en el aula. En Francisco. Martínez, & Isabel. Solano, Comunicación y relaciones sociales de los jóvenes en la red (pp. 137-151). Murcia: Marfil.
Romero, J. (2011). Las redes sociales en educación. Revista digital CIS-F. Recuperado el 24 de enero de 2014, de http://www.csi-f.es/archivos/andalucia/ensenanza/revistas/iee/Numero_44/JOSE_LUIS_ROMERO_LACAL_1.pdf.
Sáez, J. M., Lorraine, J. y Yoshiro, C. (2013). Uso de Edmodo en proyectos colaborativos internacionales en Educación Primaria. EDUTEC, Revista Electrónica de Tecnología Educativa, 43 Recuperado el 12/10/2015 de: http://edutec.rediris.es/Revelec2/Revelec43/edmodo_proyectos_colaborativos_internacionales_primaria.html.
Santos, L. (2010). La resolución de problemas matemáticos. Fundamentos cognitivos. México: Trillas.
Tejedor, J., y García-Valcácel, A. (2007). Causa del bajo rendimiento del estudiante universitario (en opinión de los profesores y alumnos). Propuesta de mejora en el marco del EEES. Revista de Educación, 37, pp. 419-442.
Vázquez, E. (2013). Microblogging con edmodo para el desarrollo de las competencias básicas del alumnado de enseñanza secundaria. un estudio de caso. Educatio Siglo XXI, 31, 1, pp. 313-334.
Veletsianos, G., y Navarrete, C. (2012). Online social networks as formal learning environments: Learner experiences and activities. The International Review of Research in Open and Distributed Learning, 13 (1), pp. 144-166.
1. Departamento de Ciencias Básicas. Pontificia Universidad Católica Madre y Maestra. República Dominicana. ivanovnnacruz@pucmm.edu.do
2. Departamento de Ciencias Básicas. Pontificia Universidad Católica Madre y Maestra. República Dominicana. angelpuentes@pucmm.edu.do
3. Facultad de Ciencias de la Educación. Departamento de Didáctica y Organización Educativa. Universidad de Sevilla. España. cabero@us.do