

Vol. 39 (Nº 28) Año 2018 • Pág. 27
Gary REYES Zambrano 1; Antonio CEDEÑO Pozo 2
Recibido: 20/02/2018 • Aprobado: 30/03/2018
RESUMEN: El estudio de técnicas de compresión de trayectorias GPS hoy día es un área activa de investigación debido al creciente desarrollo y uso de tecnologías de ubicación geográfica. Este trabajo propone un algoritmo de compresión a través de la reducción de ruido, simplificación de trayectorias, uso de información semántica y aplicación de compresión tradicional. Los resultados de las experimentaciones sobre tres conjuntos de datos evidencian un aumento de la razón de compresión, respecto a los algoritmos revisados en la literatura. |
ABSTRACT: The study of GPS trajectory compression techniques today is an active area of research due to the growing development and use of geographic location technologies. This work proposes a compression algorithm through noise reduction, trajectory simplification, use of semantic information and traditional compression application. The results of the experiments on three data sets show an increase in the compression ratio, with respect to the algorithms reviewed in the literature. |
El avance tecnológico ha propiciado que se generen necesidades en el ámbito de manejo de datos, principalmente en áreas donde existen grandes volúmenes de estos. Una de estas áreas es donde se obtiene información geoespacial, que cada día es más voluminosa (1) (2).
Esta evolución constante de las tecnologías relacionadas a la ubicación geográfica y los múltiples requerimientos de usuarios exigen precisión y exactitud a la hora de localizar un objeto, como consecuencia se produce un considerable aumento de la información de trayectorias espaciales que se requiere almacenar en las bases de datos. Esto ha traído consigo que haya un cúmulo de datos inválidos e innecesarios (9) (10). Una de las formas en la que se genera datos inexactos en las trayectorias espaciales es mediante el ruido que se detecta en las mismas, que puede traer consigo una señal no deseada, que corrompe o modifica el contenido de información a usar. Al guardar los archivos de información de las trayectorias en base de datos espaciales, consumen ciertas cantidades de espacio, acumulándose gran número de información imprecisa (3) (4). De ahí la necesidad de realizar investigaciones profundas acerca de la compresión de datos de trayectorias que ayuden a manejar la información espacial.
Hay muchos métodos de compresión de datos. Los cuales se basan en diferentes ideas, son adecuados para diferentes tipos de datos y obtienen diferentes resultados; pero todos tienen en común el mismo principio, que es comprimir los datos eliminando la redundancia de estos en el archivo de origen (2). En la compresión de trayectorias estos métodos permiten disminuir sensiblemente los puntos de la trayectoria original, lo que implica la utilización de menor espacio de almacenamiento y menor tiempo de transferencia de estos.
Para la compresión de datos se utilizan algoritmos que pueden clasificarse en dos formas: compresión sin pérdidas, que no tiene pérdida de información en los datos, y algoritmos de compresión con pérdida que eliminan cierta parte de la información, normalmente las que son redundantes (18) (19).
De los algoritmos de compresión con pérdida para trayectorias GPS que este estudio considera relevantes, se encuentra el de Douglas-Peucker (12) (14), comúnmente utilizado para adaptarse a una serie de segmentos de línea de una curva, lo que reduce los requisitos de almacenamiento. Es un algoritmo de generalización de línea, que de forma recursiva selecciona puntos de la serie original de los puntos de la trayectoria GPS (8) (15). El algoritmo divide el segmento de línea con mayor desviación en cada paso hasta que el error aproximado es menor que una tolerancia del error. La complejidad computacional es , utilizando un enfoque más complejo que implica cierres convexos. Para ajustar el conjunto de datos con más precisión, el algoritmo TD-TR modifica la fórmula de la distancia del algoritmo Douglas-Peucker, y así utilizar el componente temporal del flujo de datos de trayectoria. En este se utiliza la distancia euclidiana síncrona en lugar de la distancia perpendicular del algoritmo de Douglas-Peucker (20) (21). Otros algoritmos de compresión son los de simplificación de líneas, donde se escogen los tres primeros puntos y se traza una recta entre el primer punto y el tercero, si la distancia entre la recta y el segundo punto es mayor a la tolerancia se selecciona el segundo punto para proceder a analizar desde el segundo punto al cuarto punto; caso se elimina el segundo y se procede a repetir el proceso desde el tercer punto al quinto punto (16) (17) (19) y así sucesivamente con el resto de coordenadas. Por último, el algoritmo Visvalingam se basa en establecer una tolerancia la cual corresponderá al parámetro de área efectiva, inicialmente se establecen triángulos entre todos los puntos de las coordenadas de estudio y se calcula el área de cada uno de los triángulos, se procede a eliminar aquellos puntos cuya área sea menor a la tolerancia ingresada (5). Este proceso se lo repite con los puntos que hayan quedado hasta que el área de todos los triángulos sea mayor a la tolerancia (6) (7).
Entre los algoritmos de compresión tradicional sin pérdida, analizados en éste trabajo, se encuentran: gzip, bzip2 y Brotli. El algoritmo gzip está basado en el algoritmo Deflate que es una combinación del LZ77 y la codificación Huffman (24). El algoritmo bzip2 comprime y descomprime ficheros usando los algoritmos de compresión de Burrows-Wheeler y de codificación de Huffman (23). El algoritmo Brotli, comprime los datos utilizando una secuencia de bytes, comenzando con el primer byte en el margen derecho y procediendo al izquierdo, con el bit más significativo de cada byte a la izquierda como usual (22).
La aplicación de técnicas de compresión de datos, forman parte crucial en la fase de preparación y análisis de estos. Las mismas son un reto en sí, ya que deben conservar las propiedades estadísticas y otras características de los datos mientras los tamaños de estos son reducidos. En las trayectorias, dichas técnicas permiten comprimir la posición, dirección, velocidad, entre otras propiedades, y así reducir el tamaño de las bases de datos (10).
Teniendo en cuenta lo planteado se hace necesario la búsqueda de soluciones que permitan mejorar la compresión de datos de trayectorias respecto a los algoritmos anteriormente explicados; para esto se propone un algoritmo que permite comprimir la información espacial a través de la reducción de ruido con filtro de Kalman, simplificación de trayectorias basado en el algoritmo TD-TR y semántica, y la compresión sin pérdida de los datos resultantes utilizando Brotli. A continuación se fundamenta teóricamente los componentes que se consideran relevantes para la propuesta de dicho algoritmo.
Unos de los elementos que se tienen en cuenta para la propuesta del algoritmo es la utilización del filtro de Kalman para la reducción del ruido presente en las trayectorias espaciales, originado por los sensores u otros factores como el clima. Dicho ruido afecta la precisión de los datos, aumentando el error de los algoritmos de compresión.
Kalman es un filtro recursivo de predicción que se basa en el uso de técnicas de espacio de estado y los algoritmos recursivos. Este es un método de estimación óptimo que ha sido ampliamente utilizado en sistemas de navegación GPS (21).
El filtro de Kalman puede describirse como un proceso de dos pasos: el paso de predicción (actualización de tiempo) que hace uso del aprendizaje dinámico del sistema para anticipar el siguiente paso del sistema (actualización de la medición), que toma una nueva medición observada y la utiliza para corregir la dinámica y el estado del sistema. En el segundo paso se corrige con el modelo de observación, de modo que la covarianza del estimador de error se minimiza. En este sentido, es un estimador óptimo (17).
Fig.1
Operación del filtro de Kalman (29)
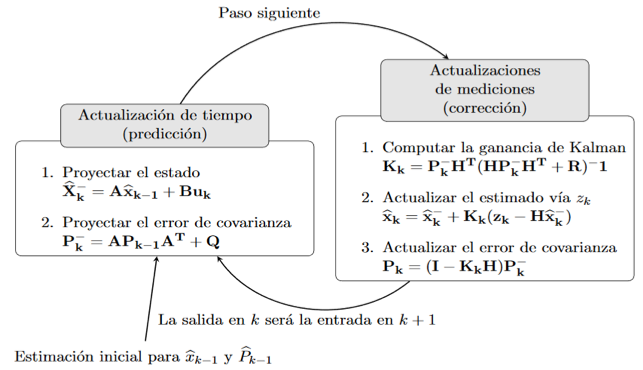
El filtro de Kalman puede disminuir el ruido presente en las trayectorias, pero este no reduce el tamaño de los datos, por lo tanto el segundo componente del algoritmo propuesto permite simplificar la trayectoria para obtener un conjunto de datos más pequeño. La simplificación de puntos en el algoritmo utiliza TD-TR e información semántica, para reducir significativamente la cantidad de puntos de la trayectoria correspondiente.
El algoritmo TD- TR es una modificación del algoritmo Douglas Peucker, en donde se le agrega el factor tiempo, para esto se calculan las coordenadas del punto en el tiempo mediante el ratio de dos intervalos de tiempo:
Fig.2
Representación del algoritmo TD-TR (21)
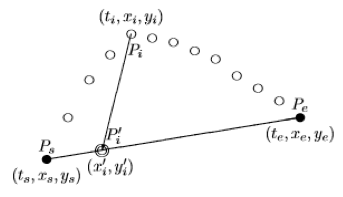

La etapa de simplificación del algoritmo propuesto, utiliza la información semántica para mejorar la precisión de los datos, así como eliminar aquellos puntos espaciales innecesarios a la hora de reconstruir una trayectoria vehicular.
La utilización de semántica en las grandes ciudades brinda posibilidades muy alentadoras, ya que una ciudad tiene una red de carretera, calles con un sentido común, áreas intransitables, edificios, casas, establecimientos, líneas de autobús, tranvía y tren, entre otros, lo cual forma una capa o red semántica. Richter (30) realiza un estudio profundo de la compresión semántica de trayectorias (STC) donde expone que un mapa es una red semánticamente anotada de aristas y nodos. Formalmente, un mapa es descrito por:
M = (VT, ET, VG, EG)
VT es un conjunto de vértices topológicos. Estas son las intersecciones de una red de transporte que definen los enlaces entre las otras entidades topológicas. ET es el conjunto de aristas topológicas entre los elementos de VT. La mayoría de los algoritmos de planificación de trayectoria trabajan en los elementos de VT y ET, que se denomina gráfico de red. Esta es también la compresión del gráfico y la descompresión de las trayectorias en su mayoría de trabajo. Sin embargo, para algunas operaciones, estos procesos necesitan utilizar la geometría de la configuración de red. Esta geometría es descrita por VG, EG, los conjuntos de vértices geométricos y aristas. Con estos conjuntos se describe el diseño real de las entidades espaciales en el entorno. La correspondencia de mapas funciona en la representación geométrica de calles (aunque enfoques sofisticados usan la representación topológica en paralelo), y ángulos de giro, es decir, ángulos entre pares de calles, se determinan en este nivel (11) (13). Para cada borde topológico hay una secuencia correspondiente de aristas. La topología abstrae de la geometría a la conexión. En la Figura 3, el borde topológico eT1T2, que conecta los vértices topológicos vT1 y vT2, abstrae de la secuencia de cinco aristas geométricos eG1 a eG5 que describen el curso entre los vértices geométricos vG1 y vG2. Se aprecia que los vértices topológicos siempre coinciden con los vértices geométricos (los primeros son un subconjunto de estos últimos), pero las aristas topológicas no necesitan corresponder a las aristas geométricas.
Fig.3
Semántica de las trayectorias (30)
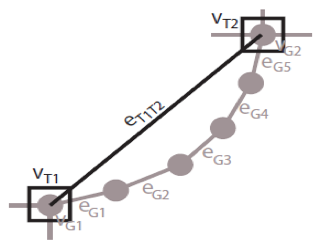
Como último elemento presente, es la forma de almacenar la información sin que se afecte los datos de la trayectoria. Para el mismo se puede utilizar el método de compresión de Brotli, es un algoritmo de compresión anunciado por Google en septiembre del 2015, el cual esta optimizado para la web, en particular pequeños documentos de texto. La compresión de Brotli es al menos tan rápida como gzip, mientras mejora significativamente la relación de compresión. (22) (25) (26).
Se realiza una propuesta de solución de un algoritmo de compresión donde se tienen en cuenta estos elementos que podrían mejorar la eficacia de los datos de trayectoria basados en el algoritmo top down time ratio (TD-TR). Estos elementos son la reducción del ruido, la simplificación de puntos de la trayectoria con el uso de TD-TR, el uso de información semántica y compresión tradicional sin pérdida. Quedando representado el algoritmo desarrollado (GR-B) con una secuencia de pasos, los cuales se resumen a continuación:
En Kalman inicialmente se construye el modelo, el cual está estrechamente relacionado con la trayectoria a analizar, de esta manera el filtro se ajusta a la trayectoria dada.
Para construir el modelo se utiliza las siguientes funciones:
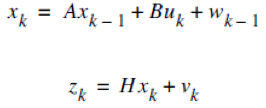
A continuación se procede a inicializar los valores del proceso basado en los valores del primer punto de latitud y longitud de la trayectoria. Para esto se utiliza las siguientes funciones de predicción o corrección.
Fig.4
Inicializar valores en Kalman
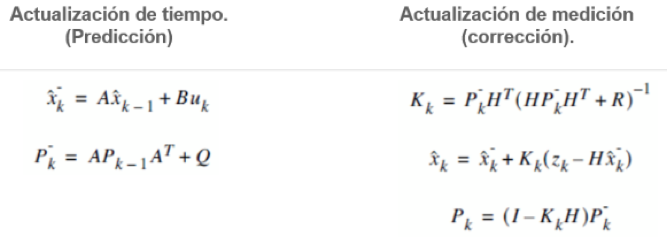
Después de reunir toda la información necesaria e inicializar los valores, se repiten las estimaciones. Cada estimación de un punto está basado en la entrada del punto anterior. El proceso iterativo del filtro de Kalman se descompone en dos etapas: (1) la predicción del estado a partir del estado anterior y las ecuaciones dinámicas y (2) la corrección de la predicción usando la observación del estado actual (Fig.1).
En el segundo paso del algoritmo GR-B se procede a simplificar los puntos de la trayectoria procesada por Kalman. La simplificación de puntos utiliza TD-TR e información semántica, para reducir significativamente la cantidad de puntos de la trayectoria correspondiente.
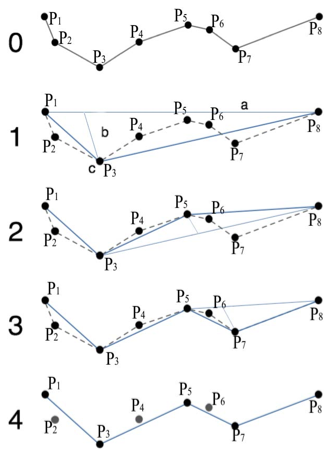
La etapa de simplificación comienza trazando el segmento de línea inicial entre el primero y el último punto. Luego calcula por medio de la distancia euclidiana sincrónica, las distancias de todos los puntos al segmento de línea e identifica el punto más alejado del segmento de línea (o la máxima distancia) y lo marca para mantenerse.
Si la distancia del punto seleccionado al segmento de línea es menor que la tolerancia definida se descartan todos los puntos que no estén marcados, en caso contrario selecciona el punto marcado para evaluarlo con la capa semántica y continúa dividiendo el segmento lineal con éste punto (Fig.5). Dicho procedimiento se ejecuta de manera recursiva hasta que el valor sea menor que la tolerancia o no se pueda dividir más el segmento de línea.
Fig.5
Simplificación de puntos utilizando
distancia euclidiana sincrónica
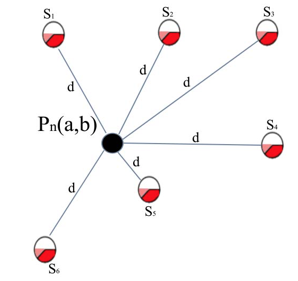
Como se había mencionada en caso de que el punto sea marcado, este se evalúa con la capa semántica (descrita posteriormente) para agregarlo o no a la trayectoria final simplificada. Para evaluar un punto marcado se calcula la distancia del circulo máximo de este a todos los puntos semánticos, el cual es aceptado si dicha distancia calculada al punto semántica más cercano es menor que la tolerancia semántica (Fig 6).
Fig.6
Evaluación de un punto con la capa semántica
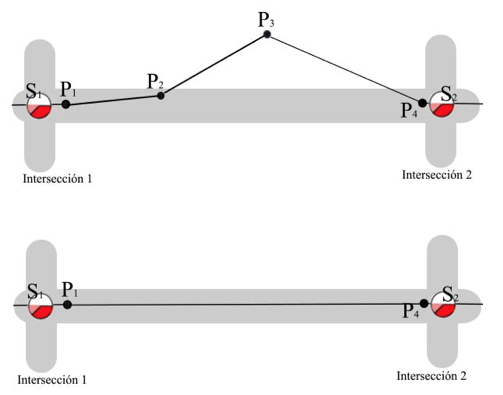
La capa semántica utilizada en el algoritmo es la de intersección de calles, esta se usa para descartar aquellos puntos que están entre dos intersecciones. Como se observa en la Fig.7 los puntos de la trayectoria p2 y p3 se eliminan manteniendo sólo los más cercanos a los puntos semánticos correspondientes a intersecciones, así se guardan solo los puntos necesarios para trazar la trayectoria de un vehículo.
Fig.7
Capa semántica de intersección de calles
La tolerancia semántica definida para cada caso debe ser mayor que el margen de error de los dispositivos GPS, el cual oscila los 5 metros, así se asegura que el algoritmo trabaje obviando el error de los GPS. A mayor tolerancia semántica se incrementa la posibilidad de aceptar más puntos.
La distancia utilizada al comprar los puntos con la capa semántica es “la distancia del círculo máximo” la cual permite realizar cálculos más exactos, ya que la distancia entre dos puntos en el espacio euclidiano es la longitud de una línea recta entre ellos, pero en la esfera no hay líneas rectas. En espacios con curvatura (como es el caso de la forma del planeta Tierra), las líneas rectas son reemplazadas por geodésicas. Las geodésicas en la esfera son círculos en la esfera cuyos centros coinciden con el centro de la esfera, y se llaman grandes círculos. Para calcular la distancia del círculo máximo (D) entre dos coordenadas se usa la siguiente ecuación:
Donde:
a y b = latitudes en grados.
| c | = el valor absoluto de la diferencia de longitud entre las coordenadas respectivas.
En el último paso, se aplica el método de compresión sin pérdida Brotli, el cual permite guardar los datos de manera íntegra y ocupando menor espacio en disco para su posterior utilización.
A continuación se realizan un conjunto de experimentos para validar los resultados del algoritmo GR-B.
En el siguiente experimento se procede a evaluar la razón de compresión y margen de error del algoritmo desarrollado (Fig.8).
Fig.8
Comparación: GR vs TD-TR.
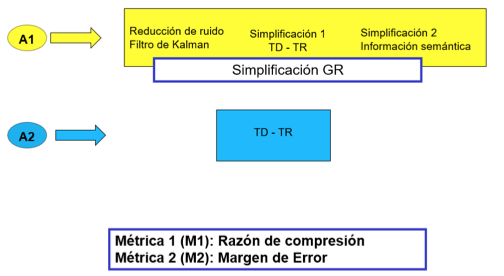
Prueba Shapiro-Wilk’s
Existen varios métodos para comprobar el ajuste a la distribución normal, entre los más conocidos se encuentran las pruebas de Kolmogorov-Smirnov y Shapiro-Wilk’s. Este último es ampliamente recomendado, y el que se utiliza en la presente investigación. En la Tabla 1 se aplican a los resultados obtenidos para las variables: margen de error y razón de compresión:
Tabla 1
Resultados de Shapiro-Wilk’s para el experimento 1.
Pruebas |
Cantidad de puntos |
Cantidad de trayectorias |
Supuesto de normalidad (Razón de compresión) |
Supuesto de normalidad (Margen de error) |
Supuesto de normalidad (Razón de compresión) |
Supuesto de normalidad (Margen de error) |
1 |
550 - 1200 |
45 |
Se rechaza Ho |
Se acepta Ho |
Se rechaza Ho |
Se acepta Ho |
2 |
650 - 1200 |
42 |
Se rechaza Ho |
Se acepta Ho |
Se rechaza Ho |
Se acepta Ho |
3 |
750 - 1200 |
42 |
Se rechaza Ho |
Se acepta Ho |
Se rechaza Ho |
Se acepta Ho |
4 |
1000 - 3000 |
42 |
Se rechaza Ho |
Se acepta Ho |
Se rechaza Ho |
Se acepta Ho |
5 |
2000 |
244 |
Se rechaza Ho |
Se acepta Ho |
Se rechaza Ho |
Se acepta Ho |
6 |
2000 - 4000 |
42 |
Se rechaza Ho |
Se acepta Ho |
Se rechaza Ho |
Se acepta Ho |
7 |
4000-9000 |
39 |
Se rechaza Ho |
Se acepta Ho |
Se rechaza Ho |
Se acepta Ho |
Al realizar la prueba para comprobar el supuesto de normalidad de los resultados obtenidos para la variable razón de compresión, se rechaza la hipótesis nula: por lo tanto los valores no se ajustan a una distribución normal. De la misma manera se observa que al realizar el test para comprobar el supuesto de normalidad para el margen de error, se acepta la hipótesis nula, por lo tanto los valores de la muestra se ajustan a una distribución normal.
La prueba de Mann-Whitney es una prueba no paramétrica que permite comparar dos muestras independientes. Tres investigadores, Mann, Whitney y Wilcoxon, perfeccionaron por separado una prueba no paramétrica muy similar que puede determinar si las muestras pueden considerarse idénticas o no sobre la base de sus rangos.
El resultado de aplicar dicha prueba a la razón de compresión se puede ver en la Fig.10.
Fig.9
Resultados de las pruebas Mann-Whitney.
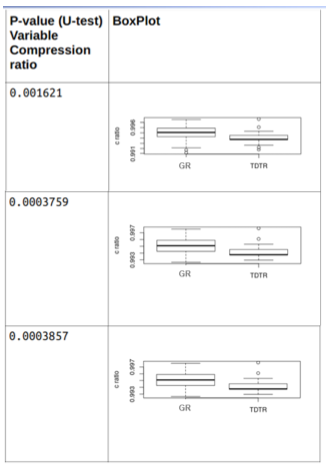
Se observa que todos los valores (p-values) son inferiores a 0.05, lo que significa que hay diferencias significativas de acuerdo a la prueba aplicada con un 95% de confianza. Y haciendo una inspección visual de las gráficas de la Figura 9, se puede apreciar que los valores de la mediana son superiores para el algoritmo GR.
Fisher’s test es una prueba estadística utilizada para determinar si hay asociaciones no aleatorias entre dos variables categóricas. La hipótesis nula para la prueba es que no hay asociación entre las filas y columnas de la tabla 2 × 2, de modo que la probabilidad de que un sujeto esté en una fila particular no se vea influenciado por estar en una columna particular. Si las columnas representan el grupo de estudio y las filas representan el resultado, entonces la hipótesis nula podría interpretarse como la probabilidad de que un resultado particular no esté influenciado por el grupo de estudio, y la prueba evalúa si los dos grupos de estudio difieren en las proporciones con cada resultado (31).
Student’s test es un método estadístico para probar hipótesis sobre la media de una muestra pequeña, la cual es extraída de una población distribuida normalmente cuando se desconoce la desviación estándar de la población. Es habitual formular una hipótesis nula, que establece que no existe una diferencia efectiva entre la media de la muestra observada y la media de la población hipotética o declarada, es decir, que cualquier diferencia medida se debe solo al azar (32).
El resultado de aplicar las pruebas Fisher’s test y Student’s test a los resultados obtenidos para la variable margen de error, se puede ver en la Tabla 2.
Tabla 2
Comparación de medias Student(T-test)
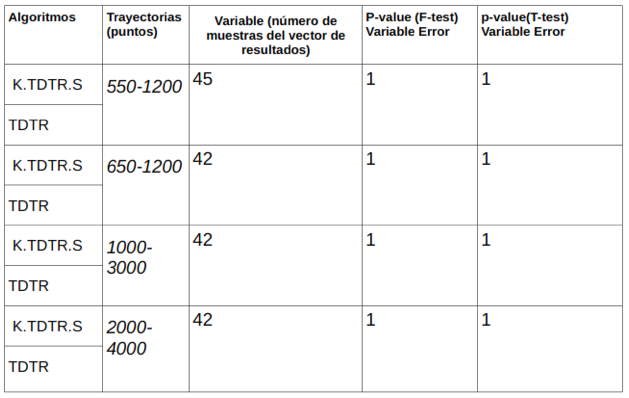
Se observa que para comprobar el supuesto de la homogeneidad de las varianzas se aplica primero, Fisher’s test, al observar que los valores de p-value obtenidos son mayores que 0.05 se asume la homogeneidad mencionada.
Una vez comprobado el supuesto de homogeneidad se usa Student’s test para comparar las medias de los vectores de resultados obtenidos para la variable error, al analizar los valores de p-value obtenidos, igualmente se obtienen valores mayores que 0.05, por lo que se puede concluir que las medias de los grupos que se comparan son significativamente similares. Todas las pruebas se realizan para un 95% de confianza.
Luego de realizar el test de hipótesis a los resultados obtenidos para la variable: razón de compresión, se comprueba que todos los valores (p-value) son inferiores a 0.05, lo que significa que hay diferencias significativas. En las gráficas de cajas (Figura 10) se aprecian que los valores de las medias son superiores para la simplificación GR.
Luego de realizar el test de hipótesis a los resultados obtenidos para la variable: margen de error, se comprueba que las medias de los grupos que se comparan son significativamente similares. Todas las pruebas se realizan para un 95% de confianza.
Se evidencia que la razón de compresión de la simplificación GR es superior a la simplificación de TD-TR
Se evidencia que el margen de error se mantiene, comparando la simplificación GR con respecto a la simplificación TD-TR.
En el siguiente experimento se procede a evaluar la razón de compresión del algoritmo desarrollado y validar con pruebas estadísticas el desempeño de los algoritmos de compresión sin perdida como brotli, bzip2, gzip o xz. El experimento se encuentra representado en la Fig.10.
Fig.10
Comparación: GR y algoritmos de compresión sin pérdida.
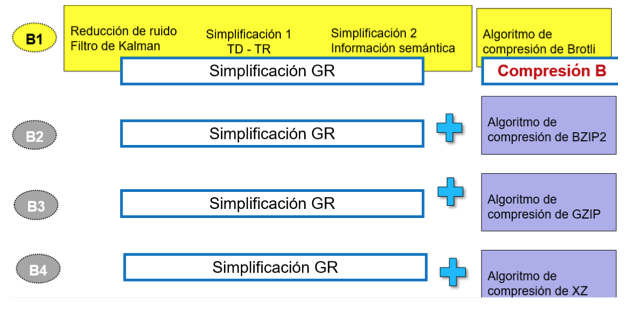
Prueba de Shapiro-Wilk’s
Tabla 3
Resultados de Shapiro-Wilk’s para el experimento 2.
Pruebas |
Cantidad de puntos |
Cantidad de trayectorias |
B1- Supuesto de normalidad (Razón de compresión) |
B2- Supuesto de normalidad (Razón de compresión) |
B3- Supuesto de normalidad (Razón de compresión) |
B4- Supuesto de normalidad (Razón de compresión) |
1 |
300 - 2500 |
300 |
Se rechaza Ho |
Se rechaza Ho |
Se rechaza Ho |
Se rechaza Ho |
2 |
310 - 4000 |
300 |
Se rechaza Ho |
Se rechaza Ho |
Se rechaza Ho |
Se rechaza Ho |
3 |
320 - 2000 |
300 |
Se rechaza Ho |
Se rechaza Ho |
Se rechaza Ho |
Se rechaza Ho |
4 |
360 - 2000 |
300 |
Se rechaza Ho |
Se rechaza Ho |
Se rechaza Ho |
Se rechaza Ho |
Se puede definir como hipótesis nula que “los grupos de muestran se ajustan a una distribución normal”, de tal forma que si la prueba arroja una diferencia significativa no existe ajuste a la distribución normal.
Se observa que al realizar la prueba para comprobar el supuesto de normalidad en los resultados obtenidos para la variable razón de compresión, se rechaza la hipótesis nula y los valores de la muestra no se ajustan a una distribución normal.
Fig.11
Resultados de la prueba Kruscal-Wallis
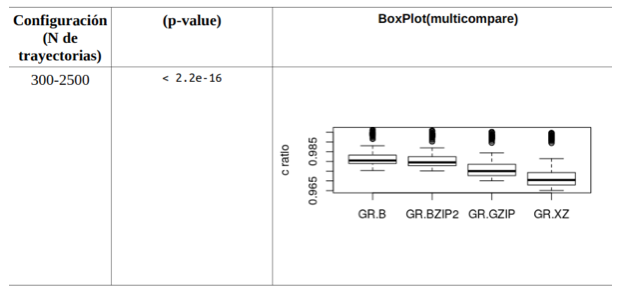
Se observa que todos los valores (p-values) son inferiores a 0.05, lo que significa que hay diferencias significativas de acuerdo al test aplicado con un 95% de confianza. Y haciendo una inspección visual de las gráficas presentes en la misma Tabla, se puede apreciar que los valores de la mediana son superiores para el algoritmo GR-B.
Resultados del experimento 2
La razón de compresión del algoritmo GR-B (utilizando compresión de Brotli) es mejor con respecto a las otras variantes del algoritmo GR (utilizando otros algoritmos de compresión que se consideran relevantes).
La utilización del filtro de Kalman y la información semántica junto con TD-TR, permite lograr un algoritmo más eficaz, el cual eleva la tasa de compresión de TD-TR a niveles superiores. Además dichos procedimientos disminuyen el ruido de la trayectoria dada, posibilitando obtener datos con un menor margen de error.
El nuevo algoritmo propuesto (GR-B) para la compresión de trayectorias GPS manifiesta una mejor eficacia.
Muckell, J., Hwang, J. H., Patil, V., Lawson, C. T., Ping, F., & Ravi, S. S. (2011, May). SQUISH: an online approach for GPS trajectory compression. In Proceedings of the 2nd International Conference on Computing for Geospatial Research & Applications (p. 13). ACM.
Salomon, David. Data Compression. Third Edition. 2004. 0-387-40697-2.Julier, S. J., & Uhlmann, J. K. (1997, April). A new extension of the Kalman filter to nonlinear systems. In Int. symp. aerospace/defense sensing, simul. and controls (Vol. 3, No. 26, pp. 182-193).
Harvey, A. C. (1990). Forecasting, structural time series models and the Kalman filter. Cambridge university press.
Meratnia, N., & Rolf, A. (2004, March). Spatiotemporal compression techniques for moving point objects. In International Conference on Extending Database Technology (pp. 765-782). Springer, Berlin, Heidelberg.9. Tan, Haoyu. A HADOOP-BASED STORAGE SYSTEM FOR BIG SPATIO-TEMPORAL DATA ANALYTICS. s.l. : The Hong Kong University of Science and Technology, 2012.
Garcia Tarira, M. F. (2017). Análisis de Algoritmos de Compresión: Simplificación de Lineas Douglas-Peucker, TD-TR, Visvalingam (Doctoral dissertation, Universidad de Guayaquil. Facultad de Ciencias Matemáticas y Físicas. Carrera de Ingeniería en Sistemas Computacionales).
Miranda Gallegos, J. L. (2017). Análisis de Comparación de Rendimiento del Algoritmo de Douglas-Peucker con la Incorporación del Filtro de Kalman (Doctoral dissertation, Universidad de Guayaquil. Facultad de Ciencias Matemáticas y Físicas. Carrera de Ingeniería en Sistemas Computacionales).
Zambrano, G. R., & Veliz, R. N. H. (2016). Aplicaciones de algoritmos de trayectorias GPS en gadgets/[GPS trajectories algorithms applications in gadgets]. International Journal of Innovation and Applied Studies, 16(3), 549.
Giannotti, F., Nanni, M., Pinelli, F., & Pedreschi, D. (2007, August). Trajectory pattern mining. In Proceedings of the 13th ACM SIGKDD international conference on Knowledge discovery and data mining (pp. 330-339). ACM.
Wang, T. (2013). An Online Data Compression Algorithm for Trajectories (An OLDCAT). International Journal of Information and Education Technology, 3(4), 480.
Lawson, C. T., Ravi, S. S., & Hwang, J. H. (2011). Compression and mining of GPS trace data: new techniques and applications. Technical Report Region II University Transportation Research Center.
Meratnia, N., & De By, R. A. (2003, October). A new perspective on trajectory compression techniques. In Proc. ISPRS Commission II and IV, WG II/5, II/6, IV/1 and IV/2 Joint Workshop Spatial, Temporal and Multi-Dimensional Data Modelling and Analysis.
Chen, M., Xu, M., & Franti, P. (2012, April). Compression of GPS trajectories. In Data Compression Conference (DCC), 2012 (pp. 62-71). IEEE.
Douglas, D. H., & Peucker, T. K. (1973). Algorithms for the reduction of the number of points required to represent a digitized line or its caricature. Cartographica: The International Journal for Geographic Information and Geovisualization, 10(2), 112-122.
Koegel, M., Baselt, D., Mauve, M., & Scheuermann, B. (2011, June). A comparison of vehicular trajectory encoding techniques. In Ad Hoc Networking Workshop (Med-Hoc-Net), 2011 The 10th IFIP Annual Mediterranean (pp. 87-94). IEEE.
Muckell, J., Olsen, P. W., Hwang, J. H., Ravi, S. S., & Lawson, C. T. (2013, July). A framework for efficient and convenient evaluation of trajectory compression algorithms. In Computing for Geospatial Research and Application (COM. Geo), 2013 Fourth International Conference on (pp. 24-31). IEEE.
Zheng, Y., & Zhou, X. (Eds.). (2011). Computing with spatial trajectories. Springer Science & Business Media.
Muckell, J., Hwang, J. H., Lawson, C. T., & Ravi, S. S. (2010, November). Algorithms for compressing GPS trajectory data: an empirical evaluation. In Proceedings of the 18th SIGSPATIAL International Conference on Advances in Geographic Information Systems (pp. 402-405). ACM.
Potamias, M., Patroumpas, K., & Sellis, T. (2006, July). Sampling trajectory streams with spatiotemporal criteria. In Scientific and Statistical Database Management, 2006. 18th International Conference on (pp. 275-284). IEEE.
Hershberger, J. E., & Snoeyink, J. (1992). Speeding up the Douglas-Peucker line-simplification algorithm (pp. 134-143). University of British Columbia, Department of Computer Science.
Ivanov, R. (2012). Real-time GPS track simplification algorithm for outdoor navigation of visually impaired. Journal of Network and Computer Applications, 35(5), 1559-1567.
J. Alakuijala, Z. Szabadk. Brotli Compressed Data Format. s.l. : Internet Engineering Task Force (IETF, 2016. ISSN: 2070-172.
SALOMÓN, David; MOTTA, Giovanni; BRYANT, David. Compresión de datos, La referencia completa.
Abdelfattah, M. S., Hagiescu, A., & Singh, D. (2014, May). Gzip on a chip: High performance lossless data compression on fpgas using opencl. In Proceedings of the International Workshop on OpenCL 2013 & 2014 (p. 4). ACM.
Pence, W. D. (2009). Feasibility Study of using BZIP2 within the FITS Tiled Image Compression Convention.
Gilchrist, J. (2004, November). Parallel data compression with bzip2. In Proceedings of the 16th IASTED international conference on parallel and distributed computing and systems (Vol. 16, pp. 559-564).
Ziv, J. and A. Lempel. "A Universal Algorithm for Sequential Data Compression. s.l. : IEEE Transactions on Information Theory.
Alakuijala, J., Kliuchnikov, E., Szabadka, Z., & Vandevenne, L. (2015). Comparison of Brotli, Deflate, Zopfli, LZMA, LZHAM and Bzip2 Compression Algorithms. Technical report, Google, Inc.
Bianco, Julio. s.l. : Univerdad Nacional de Córdoba, 2013.
Richter, K. F., Schmid, F., & Laube, P. (2012). Semantic trajectory compression: Representing urban movement in a nutshell. Journal of Spatial Information Science, 2012(4), 3-30.
Campbell, Jenny V Freeman and Michael J. The analysus of categorical data: Fisher's Exact Test. 2011.
Annie Burns, Darryl Chamberlain Jr, Aubrey Kemp, Leslie Meadow, Harrison Stalvey and Draga Vidakovic. Students’ Understanding of Test Statistics in Hypothesis Testing.
1. Universidad de Guayaquil, Facultad de Ciencias Matemáticas y Físicas, Guayaquil, Ecuador
2. Universidad de Ciencias Informáticas, La Habana, Cuba