

Vol. 39 (Nº 37) Año 2018 • Pág. 29
Jeniffer Denisse BONILLA Bermeo 1; Yuliana Yohany LEÓN Bazan 2; Jonathan Stalin DELGADO Guerrero 3
Recibido: 12/03/2018 • Aprobado: 01/05/2018
RESUMEN: El comportamiento del consumo es un fenómeno estudiado a lo largo de la historia, sobre el cual se han desarrollado una serie de teorías económicas para predecir el comportamiento esperado del agente económico. Por otro lado, la hipótesis del ingreso permanente establece que esta predicción depende de noticias inesperadas que alteran su comportamiento, por lo que tiende a ser impredecible. Para el presente estudio se evaluó el poder explicativo de las variables consumo, ingreso y tasa de interés para la economía ecuatoriana, obteniendo como resultado la carente significancia estadística de las mismas en el mercado local. |
ABSTRACT: Consumer behavior has been studied over the years, on which a series of economic theories have been developed to predict the expected behavior of the economic agent. On the other hand, the permanent income hypothesis states that this prediction depends on unexpected news that alter their behavior, so that, it tends to be unpredictable. For the present study the explanatory power of the variables: consumption, income and interest rate where evaluated for the Ecuadorian economy, obtaining as a result the lack of statistical significance of them in the local market. |
La conducta de los consumidores y su relación con la renta ha sido un tema de discusión dentro del campo económico desde hace más de medio siglo. Una de las teorías más reconocidas fue la “Teoría General” propuesta en 1936 por John Maynard Keynes, la cual establecía que la renta actual era el principal determinante del consumo y que el consumo medio se ve reducido en contraposición con el incremento en la renta. Los principales argumentos contra esta hipótesis enunciaban que el supuesto se cumplía en series de tiempo cortas, pero que fallaba para series temporales prolongadas.
Para el año de 1930 Irving Fisher propuso el modelo de elección inter temporal del consumo, el cual explicaba que las personas deciden su consumo actual y futuro en función de la maximización de sus beneficios, incluyendo conceptos como restricción presupuestaria y restricción crediticia. Esta teoría fue la base para el desarrollo de la “Hipótesis del ingreso permanente”.
La hipótesis de ingresos permanentes se fundamenta en la hipótesis del ciclo vital propuesta por Franco Modigliani. Este supuesto explica al consumo en función de la renta y la riqueza; y plantea que la renta varía sistemáticamente a lo largo de la vida de las personas, siendo el ahorro un mecanismo que permite trasladar altos niveles de renta en un periodo, a otros periodos subsecuentes con rentas bajas. De acuerdo a esta teoría las personas jóvenes que trabajan tienden a incrementar su ahorro, mientras que las personas jubiladas se inclinan al consumo (desahorro).
Gráfico 1
Teoría del ciclo de vida
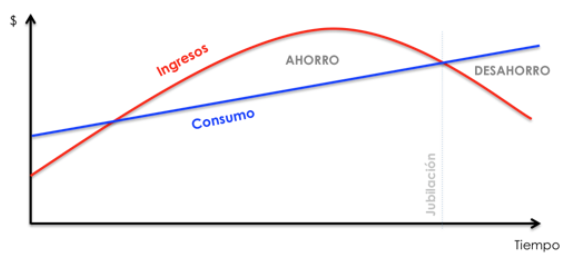
Fuente: Invependent.com
En 1957 surge un modelo que complementa a la teoría desarrollada por Modigliani, e incorpora el análisis de variaciones aleatorias y temporales de un año a otro en el comportamiento del consumidor. La hipótesis del ingreso permanente fue desarrollada por Milton Friedman y se fundamenta en que la renta muestra una distribución uniforme a lo largo de la vida de una persona, experimentando variaciones inter temporales.
De acuerdo a esta teoría, el consumo depende principalmente de la renta permanente, la cual permite a las personas mantener un hábito de consumo; y de la renta aleatoria, que puede afectar positiva o negativamente la propensión marginal a consumir, según los niveles de renta permanente. Esta aseveración está basada en el modelo inter temporal de Fisher, poniendo en relieve que el consumo depende también de las expectativas de las personas ante lo que puede suceder en un futuro, lo cual se conoce como “Expectativas Racionales”.
Finalmente el economista Robert Hall concluye que si la hipótesis de la renta permanente es correcta y si los consumidores tienen expectativas racionales, los cambios inter-temporales en el consumo se ven afectados no solo por las previsiones del futuro de las personas (que pueden ser estables), sino también por noticias inesperadas que alteran sus expectativas, y por tanto, son impredecibles. Es decir, E(gct|It-1) = E(gct), donde It-1 denota la información conocida en el periodo (t - 1); en este caso, t indica un trimestre.
Para el presente estudio se incorporaron las variables de consumo, ingreso y tasa de interés real, obteniendo una muestra de 57 datos por cada variable. Para la variable “consumo” se obtuvo información del Banco Central del Ecuador relativa al consumo real de los hogares desde el primer trimestre del año 2000 al tercer trimestre del 2014 (en miles de dólares del 2007). Para la variable “ingreso” se obtuvo información del PIB real desde el primer trimestre del año 2000 al tercer trimestre del 2014 (en miles de dólares del 2007). Para la variable tasa de interés real se consideraron las tasas pasivas mensuales de Enero del 2000 a Septiembre del 2014, descontando la inflación de estos periodos y estableciendo un promedio trimestral, para guardar consistencia con la periodicidad de la información evaluada.
Una vez obtenida la base de variables, se realizó una diferenciación logarítmica dada por la fórmula tc_x = log(x) - log(x-1), donde tc_x representa el crecimiento en la variable de estudio inter trimestral. Con este tratamiento se asume estacionalidad de la información.
Para la evaluación de la hipótesis E(gct|It-1) = E(gct) se planteó el siguiente modelo de regresión:
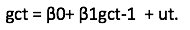
Para analizar la regresión se utilizó la prueba de significancia individual de los parámetros, en donde se plantean las siguientes hipótesis:
Ho: B1=0. La hipótesis nula indica que el crecimiento del consumo rezagado no es una variable explicativa del crecimiento del consumo actual. Es decir, E(gct|It-1) no depende de gct-1
H1: B1≠0. La hipótesis alternativa, por el contrario, no rechaza la significancia explicativa del consumo rezagado sobre el crecimiento del consumo actual.
Con el modelo de regresión expuesto, se realizó una evaluación para la muestra obtenida mediante estimadores de mínimos cuadrados ordinarios, presentándose el siguiente resultado:
Cuadro 1
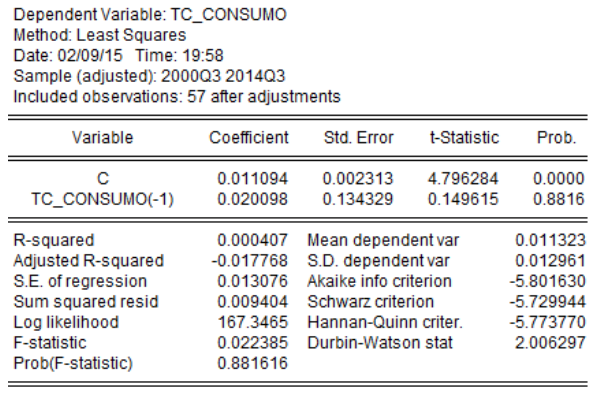
Elaborado por: Autor
Fuente: BCE
Puesto que la muestra es mayor a 30, las hipótesis se las puede contrastar utilizando dos vías: regla 2-t o análisis mediante la observación de las probabilidades asociadas a la t-estadística. La regla 2-t propone rechazar la hipótesis nula cuando la t-prueba (t-statistic para el cuadro resumen) es mayor que 2.
Para el coeficiente asociado a la variable TC_CONSUMO (-1), su t-prueba es menor que 2 por lo tanto no se rechaza la hipótesis nula y se concluye que la tasa de crecimiento del consumo rezagada un periodo no aporta a la explicación de la tasa de crecimiento del consumo actual. Adicionalmente, si solo se observan las probabilidades asociadas a la t-estadística, se aprecia que para el estimador b1 no es estadísticamente significativa, por lo que se concluye que la variable TC_CONSUMO (-1) no aporta al fenómeno en estudio.
Con el contraste de hipótesis se pudo demostrar que E(gct|It-1) no depende de gct-1. Por lo tanto, para la economía ecuatoriana, la versión de la hipótesis del ingreso permanente del consumo que afirma que el crecimiento en el consumo es impredecible si se cumple.
La hipótesis de la caminata aleatoria del consumo define que el único factor que explica el consumo es este mismo de forma rezagada. Esto no se cumple en la función estimada, puesto que el coeficiente asociado a la tasa de crecimiento del consumo rezagado un periodo no es estadísticamente significativo, es decir, el primer rezago del consumo no explica a la tasa de crecimiento del consumo.
Se aprecia que el coeficiente de determinación (R2) es bastante bajo por lo que se puede concluir que la variable considerada en la regresión no explica a la variable dependiente; es decir, menos del 1% de la variabilidad en el crecimiento del consumo se encuentra explicada por el crecimiento del consumo con un periodo de rezago.
Considerando que la base de estudio corresponde a series de tiempo, resulta necesario realizar pruebas que permitan detectar problemas de heterocedasticidad o autocorrelación que pudieran invalidar los resultados de la investigación.
Se procedió a realizar el contraste de White (productos no cruzados) para detectar problemas de Heterocedasticidad, y el contraste ARCH para Autocorrelación condicionada a la Heterocedasticidad, obteniéndose los siguientes resultados:
Cuadro 2
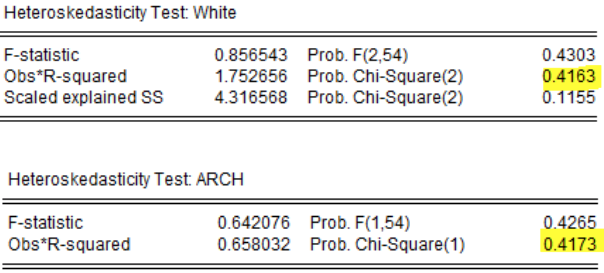
Elaborado por: Autores
Fuente: BCE
Para estas pruebas se considera como la hipótesis nula la homocedasticidad y la no autocorrelación condicionada a la Heterocedasticidad; y como hipótesis alternativa, que sí existen estos problemas, en cuyo caso se debería realizar un tratamiento especial a las variables. Para ambos contrastes las probabilidades no son significativas puesto que el valor p es superior a 0.1, permaneciendo en la zona de confianza; por lo tanto, no se rechaza la hipótesis nula: homocedasticidad para el primer caso, y para el segundo, no existe Autocorrelación condicionada a la Heterocedasticidad (por consiguiente, no se debería de utilizar modelos más complejos tipo ARCH, GARCH, etc.).
Como test adicional para evaluar si existen problemas de Autocorrelación, se procedió a realizar el correlograma de los residuos, el cual indica que las probabilidades para cada uno de los rezagos no son significativas, es decir, los residuos son ruido blanco y no existen problemas de Autocorrelación.
Cuadro 3
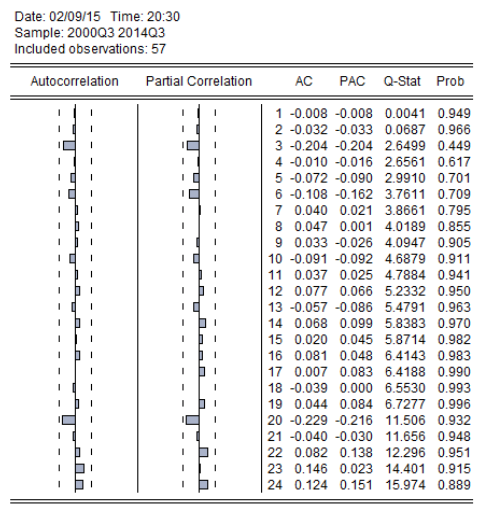
Elaborado por: Autores
Fuente: BCE
Un complemento al correlograma de los residuos, es el correlograma de los residuos al cuadrado; cuando uno de los rezagos es significativo, quiere decir que se debería construir un modelo utilizando técnicas más avanzadas de tratamiento de volatilidad tipo ARCH. Los resultados indican que no es necesario hacerlo, puesto que ninguno de sus rezagos es significativo.
-----
Cuadro 4
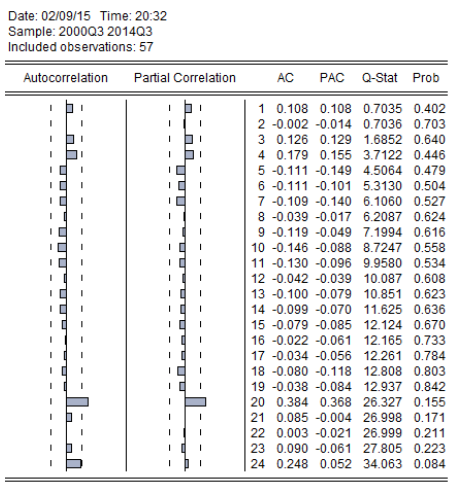
Elaborado por: Autores
Fuente: BCE
Para la evaluación de la hipótesis de ingresos permanentes y expectativas racionales se planteó el siguiente modelo de regresión:
![]()
Con el modelo de regresión expuesto, se realizó una evaluación para la muestra obtenida mediante estimadores de mínimos cuadrados ordinarios, presentándose el siguiente resultado:
Cuadro 5
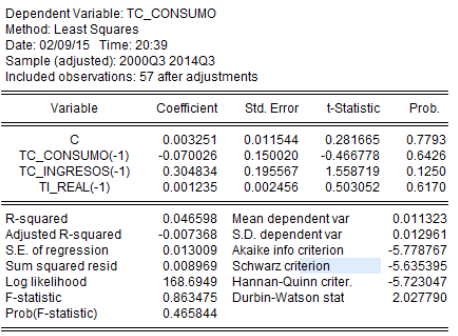
Elaborado por: Autores
Fuente: BCE
Se observa en el cuadro cinco que las probabilidades de los 4 coeficientes no son significativas con el 95% de confianza. Por otro lado, se aprecia que hubo una mejora en el coeficiente de determinación (R2), aunque este no es directamente observable por dos motivos: las variables son series de tiempo y el coeficiente de determinación es una función lineal creciente, lo que ocasiona que a medida que se incremente el número de variables, el R2 tiende a incrementarse también.
Para contrastar la significancia de las dos variables incorporadas en el modelo, se puede utilizar el test de restricciones de coeficientes Wald, el cual se expone a continuación:
Cuadro 6
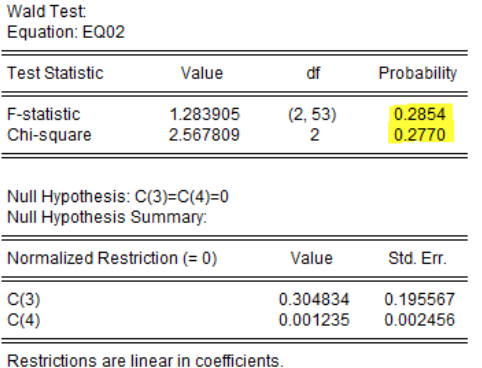
Elaborado por: Autores
Fuente: BCE
Para estas pruebas se considera como la hipótesis nula que el crecimiento del ingreso rezagado un periodo y la tasa de interés real rezagada un periodo no aportan a la explicación del crecimiento del consumo; y como hipótesis alternativa, que estas variables sí son significativas para el fenómeno de estudio. Las probabilidades, como se puede observar, están asociadas al no rechazo de la hipótesis nula, es decir, los coeficientes en conjunto son iguales a cero por lo que no aportan significativamente para la explicación de la tasa de crecimiento del consumo.
La hipótesis de ingreso permanente según Friedman plantea que el consumo depende principalmente de la renta permanente, argumentando que los periodos de elevada renta deben ser periodos de baja propensión media al consumo. Esto no pudo ser probado en la función estimada, puesto que el coeficiente asociado a la tasa de crecimiento del ingreso rezagado un periodo no es estadísticamente significativo, es decir, el primer rezago de los ingresos no explica a la tasa de crecimiento del consumo.
Con la finalidad de evaluar la existencia de una correlación fuerte (pero no perfecta) entre las variables independientes incluidas en el modelo, se realizó una prueba de multicolinealidad a través de la matriz de correlaciones y, en base a los coeficientes, se utilizó el Factor de Inflación de la Varianza FIV.
El FIV es un indicador de multicolinealidad el cual propone que si el resultado del mismo es mayor que 10, existirían indicios de un alto grado de multicolinealidad, la fórmula es la siguiente:
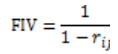
Nótese que la única combinación de los coeficientes para que el FIV sea mayor que 10 es aquella en la que el coeficiente es mayor a 0.91. La matriz de correlaciones no indica algún coeficiente superior a 0.91 por lo que no existirían problemas de multicolinealidad.
Cuadro 7
|
TC_CONSUMO(-1) |
TC_INGRESOS(-1) |
TI_REAL(-1) |
TC_CONSUMO(-1) |
1 |
0.12 |
-0.04 |
TC_INGRESOS(-1) |
0.12 |
1 |
-0.04 |
TI_REAL(-1) |
-0.04 |
-0.04 |
1 |
Elaborado por: Autores
Fuente: BCE
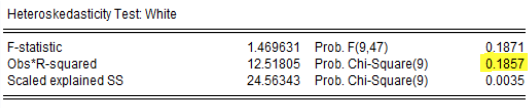
Con la finalidad de ratificar la validez de los resultados, se testeó si existe algún problema de Heterocedasticidad en el modelo planteado, utilizando el contraste White de productos cruzados con los siguientes resultados:
Cuadro 8
Elaborado por: Autores
Fuente: BCE
El valor p obtenido mediante el contraste White (productos cruzados) no es significativo, por lo que no hay evidencia suficiente para rechazar la hipótesis nula: Homocedasticidad.
Puesto que el indicador de Autocorrelación Durbin - Watson posee como restricción la no incorporación de variables rezagadas del lado derecho de la ecuación de regresión, no es directamente observable.
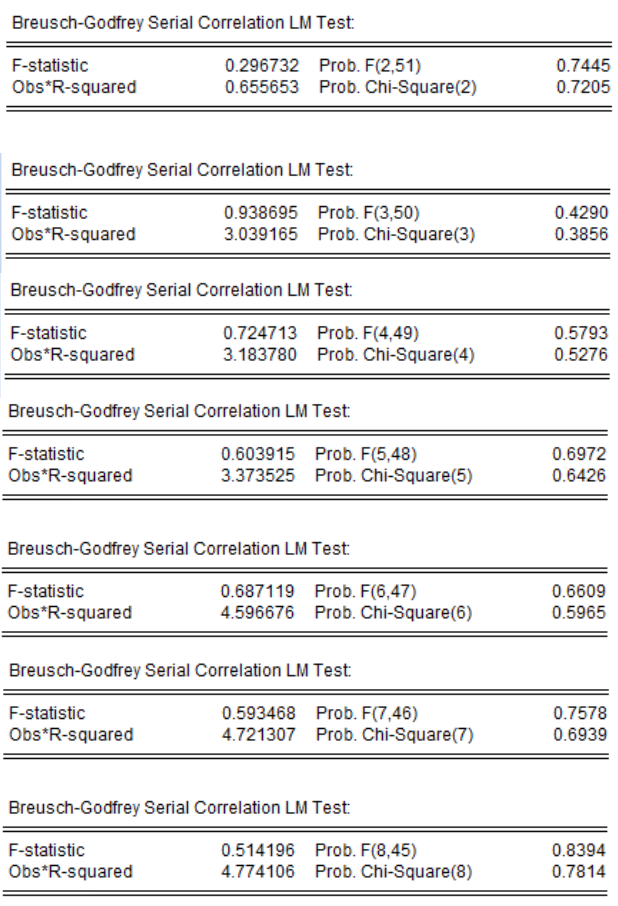
Para contrastar la autocorrelación es necesario acudir al test Breusch – Godfrey al estilo del multiplicador de Lagrange. El contraste se realizó utilizando distintos rezagos, comenzando por el octavo; los resultados del contraste se encuentran en el Anexo 2.
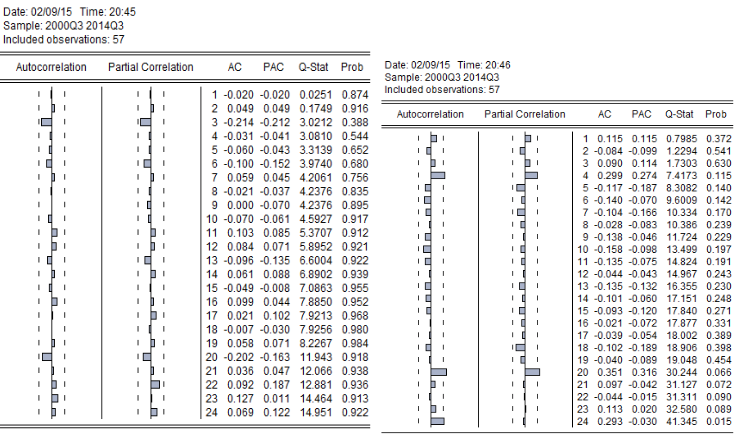
A continuación se utilizó el correlograma de los residuos obteniéndose el siguiente resultado:
Cuadro 9
Elaborado por: Autores
Fuente: BCE
El correlograma de los residuos muestra probabilidades no significativas asociadas a cada uno de sus rezagos, por lo que se puede concluir que los residuos son ruido blanco y que no existen problemas de Autocorrelación de ningún orden. Además, el correlograma de los residuos al cuadrado tampoco posee rezagos significativos por lo que no sería necesario establecer medidas para lidiar con este problema.
Con base en los resultados obtenidos, y considerando las validaciones de posibles problemas que pudiese presentar la información, se puede concluir que el ingreso y la tasa de interés rezagados un periodo no aportan a la explicación del fenómeno del crecimiento en el consumo actual en la economía ecuatoriana.
Adicionalmente, se testeó el poder explicativo del crecimiento del consumo rezagado un periodo, para determinar el comportamiento del crecimiento en el consumo actual (caminata aleatoria del consumo); no obstante, los resultados tampoco fueron significativos para explicar el fenómeno de estudio.
Por lo tanto, la versión de la hipótesis del ingreso permanente del consumo que indica que el crecimiento del consumo es impredecible (dada por la ecuación E(gct|It-1) = E(gct)), es la que mejor se ajusta al comportamiento del consumo en el Ecuador.
Banco Central de Ecuador. (2015, Febrero 1). Retrieved from www.bce.ec
GREENE, William. (2003) Econometric Analysis, fith edition. New Yersey: Prentice Hall.
GUJARATI, Damodar y PORTER, Dawn (2009). Econometría, quinta edición. México: McGraw – Hill.
HILL, Carter, GRIFIFTH, William y JUDGE, George (2001). Using Eviews For Undergraduate Econometric, second edition. New York: Wiley & Sons, INC., Publication.
Invependent. (2015, Febrero 07). Retrieved from http://www.invependent.com/.content/invPages/Teorxa_del_ciclo_de_vida
MANKIW, Gregory (2003). Macroeconomía, cuarta edición. Antoni Bosch, editor.
PÉREZ, Cesar. (2006). Problemas resueltos de econometría. España: Thomson.
WOOLDRIDGE, Jeffrey (2001). Introducción a la econometría: un enfoque moderno, segunda edición, México: Thomson Learning.
ANEXO 1
Regresiones complementarias
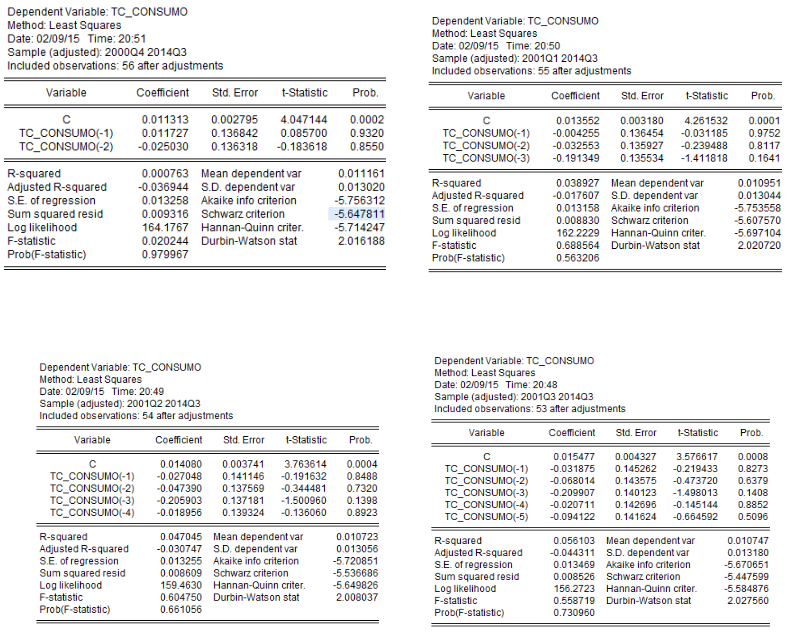
ANEXO 2
Contraste BG LM
1. Ingeniera en Ciencias Empresariales con concentración en Finanzas. CPA. Magister en Economía y Dirección de Empresas. Docente de la Facultad de Ciencias Matemáticas y Físicas de la Universidad de Guayaquil. jeniffer.bonillab@ug.edu.ec
2. Ingeniera en Sistemas Computacionales. Magister en Sistemas de Información Gerencial. Docente de la Facultad de Ciencias Matemáticas y Físicas de la Universidad de Guayaquil. yuliana.leonb@ug.edu.ec
3. Ingeniero en Sistemas, Mg. en Educación Informática, Mg. en Sistemas de Información Gerencial. Docente en la Facultad de Ciencias Matemáticas y Físicas de la Universidad de Guayaquil. Jonathan.delgadogu@ug.edu.ec